Число степеней свободы механизма
Это одно из важнейших структурных понятий. Ранее для него применялся термин “подвижность” механизма. По физическому смыслу это количество независимых движений, которые могут совершать звенья механизма. Каждой степени свободы соответствует своя обобщённая координата, т.е. число степеней свободы равно количеству обобщенных координат. Число степеней свободы пространственных механизмов вычисляется по формуле Сомова-Малышева [1, 9, 14, 18]:
(1.1)
где n – количество подвижных звеньев в механизме, pk – количество кинематических пар k -го класса. Формула (1.1) получена умозрительно. Действительно, 6n – это общее количество степеней свободы, которые имели бы n звеньев, будучи свободными, а k . pk – это количество степеней свободы, которые отнимают кинематические пары k -го класса, Пример. У механизма на рис. 1.2г четыре подвижных звена и четыре кинематические пары 5-го класса, следовательно, W = 6 . 4 – 5 . 4 = 4. Обобщенными координатами этого механизма являются параметры относительного положения звеньев j1, j2, S3, j4. И все эти движения могут происходить независимо друг от друга. Число степеней свободы плоских механизмов вычисляется по формуле Чебышева [1, 9, 14, 18]:
(1.2) где pН – количество низших, pВ – количество высших кинематических пар. В плоских механизмах кинематические пары 5-го класса всегда низшие, а 4-го класса всегда высшие. Этим и объясняется второе равенство в формуле (1.2). Пример. У механизма на рис. 1.2д три подвижных звена и четыре кинематические пары 5-го класса, следовательно W = 3 . 3 – 2 . 4 = 1. Обобщенной координатой является угол поворота j1 звена 1. В этом механизме независимым будет только вращение звена 1. Следует иметь ввиду, что формулы (1.1) и (1.2) справедливы только для механизмов без пассивных связей. Пассивная связь – это, как правило, звено, удаление которого из механизма не влияет на его кинематику, то есть с точки зрения кинематики оставшиеся звенья будут совершать те же движения. Подобные звенья вводят в меха Таким образом, прежде, чем применять формулы (1.1), (1.2) следует из механизма условно удалить все пассивные связи. В литературе можно встретить более сложные формулы для вычисления числа степеней свободы, в которые входят слагаемые, учитывающие пассивные связи. Однако использование этих зависимостей все равно требует предварительной диагностики того, какие связи являются пассивными.
|

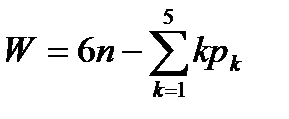
 – общее количество степеней свободы, которые отнимают все кинематические пары.
– общее количество степеней свободы, которые отнимают все кинематические пары.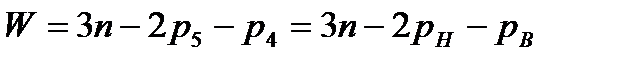
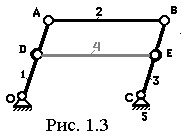 низм для увеличения его прочности или жесткости. Пример механизма с пассивной связью представлен на рис. 1.3. Очевидно, что удаление звена 4 не повлияет на характер движения звеньев 1, 2, 3. Однако, это справедливо не для любого сочетания размеров звеньев, а лишь тогда, когда l1 = l3, l2 = l4. Поэтому, непосредственное применение формулы (1.2) к этому механизму дает результат: W = 3 . 4 – 2 . 6 = 0.
низм для увеличения его прочности или жесткости. Пример механизма с пассивной связью представлен на рис. 1.3. Очевидно, что удаление звена 4 не повлияет на характер движения звеньев 1, 2, 3. Однако, это справедливо не для любого сочетания размеров звеньев, а лишь тогда, когда l1 = l3, l2 = l4. Поэтому, непосредственное применение формулы (1.2) к этому механизму дает результат: W = 3 . 4 – 2 . 6 = 0.


