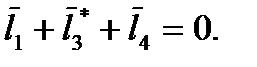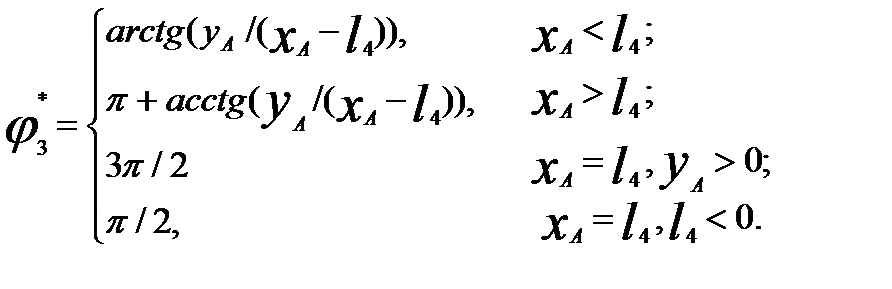Для структурных групп, связанных со стойкой
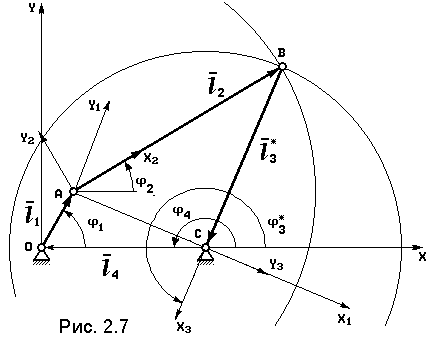
Решать задачу кинематического анализа будем методом векторных контуров, суть которого изложена в подразд. 2.2. Рассматриваться будут механизмы с входным звеном – кривошипом, но это никак не ограничивает общности, т.к. в итоговых выражениях входными кинематическими параметрами будут параметры движения входной кинематической пары и полученные результаты будут инвариантны по отношению к входному движению. 2.3.1. Трёхшарнирная структурная группа
Уравнение замкнутого векторного контура для обеих сборок:
yA + l 2 sin j2 + l 3* sin j3 = 0. Для получения явного решения этой системы рассмотрим схемы на рис. 2.7, 2.8. В системе координат AXY запишем уравнения окружностей: первая радиусом АВ с центром в шарнире А, вторая радиусом СВ, с центром в шарнире С:
(x2 – AC) 2 + y2 = BC2, Отсюда получаем координаты шарнира B в системе AX1Y1:

Знак “+” соответствует прямой сборке, “–” – обратной. Найденные xB1, yB1 преобразуем в систему OXY, как это описано в подразделе 2.4. В результате получим координаты шарнира B xB, yB. Угол для такого преобразования:

Тогда искомые углы поворота шатуна АВ и коромысла ВС:
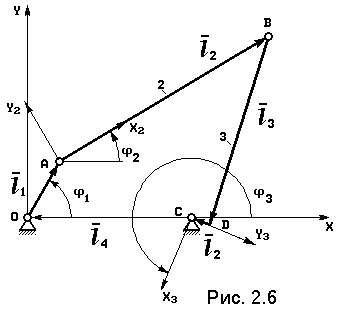
При наличии смещения CD (на рис. 2.6 показано положительное смещение) угол поворота коромысла BC: j3 = j3* + ¡; (2.14) где ¡ = arctg(CD / l 3). Для определения угловых скоростей шатуна AB w2 и коромысла BC w3 продифференцируем систему (2.9) по времени:
vAy + l 2 w2 cos j2 + l 3* w3 cos j3 = 0.
где: vAx = – l 1 w1 sin j1, vAy = l 1 w1 cos j1 – проекции скорости входного шарнира A на оси неподвижной системы координат OXY. Система (2.15) линейна относительно w2, w3, и легко разрешима, например, по формулам Крамера. Дифференцируя (2.15) по времени, получим систему уравнений для определения угловых ускорений шатуна e2 и коромысла e3:
 
где: Система (2.17) также линейна относительно неизвестных e2, e3. 2.3.2. Структурная группа "шатун - ползун";
Проецируя его на оси неподвижной системы координат OXY, получим:
l 1 sin j1 + l 2 sin j2 + l 3 sin j3 + l 4 sin j4 = 0.
Угол j4= 180O = Const. Угол j3 также не меняется, но зависит от направления смещения точки B: j3 = 90О на рис. 2.9, j3 = 270O на рис. 2.10. Обозначим: l 3* = l 3 sin j3, учитывая, что l 1cos j1 = xA, l 1sin j1 = yA – координаты входного шарнира, систему (2.17) запишем в виде:
yA + l 2 sin j2 + l 3* = 0. Так как при заданных кинематических параметрах движения входного звена угол j1, а, следовательно, и xA, yA известны, то эта система легко решается относительно неизвестных j2, l 4
l 4 = xA + l 2 cos j2. Дифференцируя систему (2.18) по времени, получим:
vAy + l 2 w2 cos j2 = 0. где: vAx, vAy – проекции скорости входного шарнира A на оси НСК OXY. Тогда угловая скорость шатуна и скорость ползуна:
vB = vAx – l 2 w2 sin j2.
где: aAx, aAy – проекции ускорения входного шарнира A на оси НСК OXY (см. уравнение (2.16). Тогда угловое ускорение шатуна и ускорение ползуна:

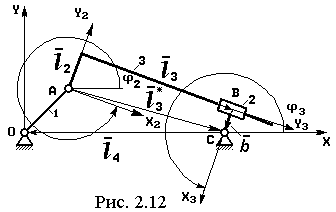
2.3.3. Кулисные структурные группы
Если занумеровать звенья так, как это показано на рис. 2.11, 2.12, то уравнение замкнутого векторного контура для обеих модификаций запишется одинаково:
yA + l 3* sin j3* = 0. Из системы (2.23) находим: (2.24) Отметим, что при вычислении по формулам (2.24) результат l 3* = 0 является признаком неработоспособности механизма если в процессе движения входное звено должно проходить положение (xA = l 4, yA = 0). Для определения угловой скорости кулисы w3* и скорости ползуна относительно кулисы v 3* продифференцируем систему (2.23) по времени: vAx
vAy + v 3* sin j3* + l 3 w3* cos j3* = 0.
где: vAx, vAy – проекции скорости входного шарнира A (см. уравнения (2.20).
Дифференцируя (2.25) по времени, получим систему уравнений для определения углового ускорения кулисы e3* и ускорения ползуна относительно кулисы a 3*:
aAy + a 3* sinj3*+ 2 v 3* w3* cosj3* + l 3* e3* cosj3* – l 3*w3*2 sinj3*= 0. где: aAx, aAy – проекции ускорения входного шарнира A на оси неподвижной системы координат OXY (см. уравнение (2.1). Кинематические параметры движения кулисы при наличии смещений l 2, b (см. рис. 2.11, 2.12) получим через параметры движения вектора l 3*, который повернут относительно вектора l 3 на угол ¡: ¡ = arcsin((b – l 2 )/ l 3*); j3 = j3* + ¡; l 3 = l 3* cos ¡. (2.27) На рис. 2.11, 2.12 показаны положительные смещения l 2 и b. Дифференцируем дважды по времени выражения для j3 и l 3: ... w3 = w3*+ ¡; e3 = e3* + ¡; . v 3 = v 3* cos ¡ – l 3* ¡ sin ¡; (2.28) .... a 3 = a 3* cos ¡ – 2 v 3* ¡ sin ¡ – l 3*(¡ sin ¡ + ¡2 cos ¡), Необходимые для вычисления по формулам (2.28) производные от ¡, определим последовательно дифференцируя первое из выражений (2.27):

2.3.4. Структурная группа "шарнир – ползун – ползун";
Уравнение замкнутого векторного контура:
Проецируя его на оси системы координат OXY получим:
xA
yA + l 11 sin j2 + l 12 sin b + l 3 sin j3 + l 4 sin j4 + l 5 sin j5 = 0.
Здесь l 1cos j1 = xA, l 1 sin j1 = yA – координаты входного шарнира A. Угол j4 = 180О = Const, углы j2, j3, j5 тоже постоянны, при этом j2 = b – p/2, j3 = b + p (b – угол между осями ползунов), а угол j5 – между осью Х и вектором l 5 зависит от направления смещения точки C: и равен 90О или 270О. Обозначив l 5* = l 5 sin j5 систему (2.30) запишем в виде:
yA + l 11 sin j2 + l 12 sin b + l 3 sin j3 + l 5* = 0. Отсюда находим неизвестные l 3, l 4 . l 3 = –(yA + l 11 sin j2 + l 12 sin b + l 5*)/sin j3; l 4 = xA + l 11 cos j2 + l 12 cos b + l 3 cos j3; Последовательно дифференцируя систему (2.31) по времени, получим уравнения для определения v 3, a 3 – скорости и ускорения скольжения ползуна В и v 4, a 4 – скорости и ускорения ползуна С: vAx + v 3 cos j3 – v 4 = 0;
Откуда v 3 = – vAy / sin j3; v 4 = vAx + v 3 cos j3. Соответственно, ускорения aAx + a 3 cos j3 – a 4 = 0; aAy + a 3 sin j3 = 0. Откуда a 3 = – aAy / sin j3; a 4 = aAx + a 3 cos j3.
где: vAx, vAy, aAx, aAy – проекции скорости и ускорения входного шарнира A. 2.3.5. Структурная группа "ползун – шарнир – ползун";
Механизм, состоящий из входного звена OA и структурной группы рассматриваемого типа представлен на рис. 2.14. Ось X неподвижной системы координат OXY направим параллельно оси ползуна C, так как в такой системе задача решается проще. Все смещения показаны положительными.
Проецируя его на оси системы OXY и учитывая, что при положительных смещениях углы j3 = 270О, j4 = 180О, получим:
l 0 sin j2 + l 1 sin j1 + l 11 sin j2 + l 12 sin j1 + l 22 – l 3 = 0, где: j2 = j1 – p /2. Из системы (2.33) находим неизвестные l 1, l 4: l 4 = l 0 cos j2 + l 1 cos j1 + l 11 cos j2 + l 12 cos j1 + l 21; l 3 = l 0 sin j2 + l 1 sin j1 + l 11 sin j2 + l 12 sin j1 + l 22, Отметим, что при j1 = 0 или j1 = 180О данная структурная группа имеет неопределенное положение, т.к. оси ползунов становятся параллельными и появляется дополнительная степень свободы. Дифференцируя систему (2.33) по времени, получим:
l 0 w1 cos j2 + l 1w1 cos j1 + v 1 sin j1 – l 2 w2 cos j2 = 0. Отсюда найдем v 1 – скорость ползуна A относительно входного звена и скорость выходного ползуна C, равную скорости точки B: v B = v 4 Дифференцируя (2.34) по времени и приводя подобные члены, получим: –e1 ((l 0 + l 2 ) sin j2 + l 1 sin j1) – w22 ((l 0 + l 2 ) cos j2 + l 1 cos j1) –
e1 ((l 0 + l 2 ) cos j2 + l 1 cos j1) – w22 ((l 0 + l 2 ) sin j2 + l 1 sin j1) + + 2 v 1w1 cos j1 + a 1 sin j1 = 0.
Отсюда находим a 1 – ускорение ползуна A относительно входного звена и ускорение выходного ползуна a C = a B = a 4. Как следует из полученных выражений, особенностью расчета данной структурной группы является необходимость задания кинематических параметров движения входного звена j1, w1, e1.
|


 ,
, 




 ,
,  – проекции ускорения входного шарнира А на оси системы OXY.
– проекции ускорения входного шарнира А на оси системы OXY.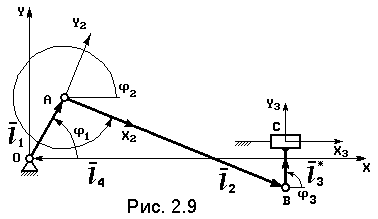


 Дифференцируя (2.20) по времени, получим систему уравнений для определения ускорений:
Дифференцируя (2.20) по времени, получим систему уравнений для определения ускорений: