Передаточные функции, передаточное отношение
Здесь мы коснёмся только вопросов, связанных с передаточными функциями по скорости. 2.6.1. Передаточная функция
У этой функции есть две характеристики: её форма и её размах v Bm. Форма зависит от сочетания размеров механизма, то есть от его внутренних свойств. А размах – от величины угловой скорости входного кривошипа w1, то есть от внешнего сигнала. При решении очень многих задач, и не только в механике, желательно разделить – что зависит от внутренних свойств объекта, а что – от внешних факторов. Скорость это первая производная от перемещения по времени: v B = dx B / dt. В этом выражении внутренние и внешние свойства перемешаны. Разделим их, расписав полную производную по времени через частные – по обобщённой координате и времени:
Теперь первый сомножитель S B’, названный передаточной функцией, содержит информацию о внутренних свойствах механизма, а второй w1 – о внешнем сигнале. Физический смысл передаточной функции становится очевиден, если её записать так: S B’ = v B / w1, то есть это скорость ползуна при w1 = 1. Следовательно, для её построения достаточно произвести кинематический анализ механизма, например, методом векторных контуров при w1 = 1, e1 = 0. 2.6.2. Передаточное отношение
Дальнейшие действия аналогичны тому, что выполнялось для передаточных функций. Собственно передаточное отношение это вид передаточной функции. Форма графика w2 зависит от сочетания размеров механизма, то есть от его внутренних свойств. А размах – от величины угловой скорости входного кривошипа w1, то есть от внешнего сигнала. Угловая скорость это первая производная от угла поворота по времени: w2 = d j2 / dt. В этом выражении внутренние и внешние свойства перемешаны. Разделим их, расписав полную производную по времени через частные – по обобщённой координате и времени:
Теперь первый сомножитель i 21, названный передаточным отношением, содержит информацию о внутренних свойствах механизма, а второй w1 – о внешнем сигнале. Физический смысл передаточного отношения становится очевиден, если его записать так: i 21 = w2 / w1, то есть это угловая скорость шатуна при w1 = 1. Следовательно, для её построения достаточно произвести кинематический анализ механизма, например, методом векторных контуров при w1 = 1, e1 = 0. Обобщим полученный результат. Передаточным отношением от звена с номером j к звену с номером k называется отношение угловых скоростей звеньев: i jk = wj / wk. Для рассмотренного рычажного механизма передаточное отношение i 21 это величина переменная, а, например, для подавляющего большинства зубчатых механизмов – это константа. Но этот вопрос рассмотрен в соответствующем разделе данного пособия. 2.7. Графо-аналитический метод планов [2]
Схема для расчёта этим методом кинематики четырёхшарнирного механизма представлена на рис. 2.20. Построение плана скоростей четырёхшарнирного механизма 1. Выбранном масштабе вычерчиваем план механизма в расчётном положении (см. рис. 2.20а). 2. Параметры движения входного кривошипа OA известны по постановке задачи, вычисляем величину скорости конца кривошипа v A = w1 l 1 3. Полагая, что кривошип является абсолютно твёрдым телом, направляем вектор Определим скорость шарнира B Он принадлежит одновременно шатуну AB и коромыслу BC. (.)B ÎAB, поэтому, если принять (.)A за полюс, то скорость (.)B представима как
где С другой стороны, (.)B Î BC. Тогда скорость точки B представима как
где В данном случае v C = 0, поэтому
(2.38)
Решим её графически путём построения плана скоростей, который представляет собой графическое представление системы (2.38). 1. Выбираем масштабный коэффициент для плана скоростей k V, имеющий размерность 2. Величина вектора 3. Величина вектора 4. Точка пересечения этих линий удовлетворяет обоим уравнениям системы (2.38). Следовательно, она и является её решением. Обозначаем найденные векторы – рис. 2.20в. Величины найденных векторов определим, измеряя их на плане и умножая на масштабный коэффициент. Величины угловых скоростей: w2 = v BA/ l AB, w3 = v B/ l BC. Построение плана ускорений четырёхшарнирного механизма при постоянной угловой скорости кривошипа 1. Выбранном масштабе вычерчиваем план механизма в расчётном положении (см. рис. 2.20а,г). 2. Параметры движения входного кривошипа OA известны по постановке задачи, вычисляем величину ускорения конца кривошипа, которая при w1 = Const имеет только нормальную составляющую a A = a A n = w12 l 1 3. Полагая, что кривошип является абсолютно твёрдым телом, направляем вектор Определим ускорение шарнира B Он принадлежит одновременно шатуну AB и коромыслу BC.
где С другой стороны, (.)B Î BC. Тогда ускорение точки B представима как
где В данном случае a C = 0, поэтому
(2.39) Решим её графически путём построения плана ускорений. План ускорений представляет собой графическое представление системы (2.39). 1. Выбираем масштабный коэффициент для плана ускорений ka, имеющий размерность 2. Величину нормальной составляющей a BAn можно вычислить: a BAn = v BA2/ l 2 = w22 l 2. Направлено она вдоль оси шатуна 2 от (.)B к (.)A. Откладываем её на плане (см. рис. 2.20д). 3. Касательная составляющая a BAt нам пока не известна, но известно, что её линия действия перпендикулярна оси шатуна AB. В соответствии с первым уравнением системы (2.39) проводим её на плане скоростей из конца вектора a BAn перпендикулярно шатуну AB – тонкая зелёная линия на рис. 2.20д. 4. Величину нормальной составляющей a BCn можно вычислить: a BCn = v B2/ l 3 = w32 l 3. Направлена она вдоль оси коромысла 3 от (.)B к (.)C. Откладываем её на плане ускорений из его полюса, т.к. первое слагаемое в правой части второго уравнения системы (2.39) равно нулю (см. рис. 2.20д). 5. Касательная составляющая a BCt пока тоже не известна, но известно, что её линия действия перпендикулярна оси коромысла BC. Проводим её на плане ускорений из конца вектора a BCn – тонкая синяя линия на рис. 2.20д. 6. Точка пересечения линий удовлетворяет обоим уравнениям системы (5.13). Следовательно, она и является её решением. Обозначаем найденные векторы – рис. 2.20е. Векторные суммы нормальных и касательных составляющих являются полными ускорениями точек
Величины найденных векторов определим, измеряя их на плане и умножая на масштабный коэффициент. Величины угловых ускорений: e2 = a BAt/ l AB, e3 = a BCt/ l BC.
|






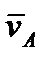 перпендикулярно оси кривошипа (см. рис. 2.20а).
перпендикулярно оси кривошипа (см. рис. 2.20а).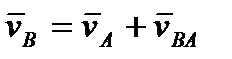
 – скорость (.)B относительно (.)A.
– скорость (.)B относительно (.)A.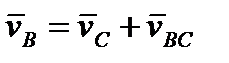
 – скорость (.)B относительно (.)C.
– скорость (.)B относительно (.)C. .
. Таким образом, для определения
Таким образом, для определения  мы получили систему векторных уравнений:
мы получили систему векторных уравнений: , и из полюса плана p V в этом масштабе откладываем вектор
, и из полюса плана p V в этом масштабе откладываем вектор  (см. рис. 2.20б).
(см. рис. 2.20б). вдоль оси кривошипа от (.)A к (.)O (см. рис. 2.20г).
вдоль оси кривошипа от (.)A к (.)O (см. рис. 2.20г). (.)B ÎAB, поэтому, если принять (.)A за полюс, то ускорение (.)B представимо как
(.)B ÎAB, поэтому, если принять (.)A за полюс, то ускорение (.)B представимо как – ускорение (.)B относительно (.)A,
– ускорение (.)B относительно (.)A,  – его нормальная и касательная составляющие.
– его нормальная и касательная составляющие.
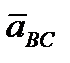 – ускорение (.)B относительно (.)С,
– ускорение (.)B относительно (.)С,  – его нормальная и касательная составляющие.
– его нормальная и касательная составляющие.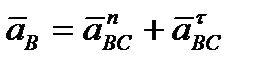 .
. Таким образом, для определения
Таким образом, для определения  мы получили систему векторных уравнений:
мы получили систему векторных уравнений: , и из полюса плана pa в этом масштабе откладываем вектор
, и из полюса плана pa в этом масштабе откладываем вектор  (см. рис. 2.20д).
(см. рис. 2.20д).



