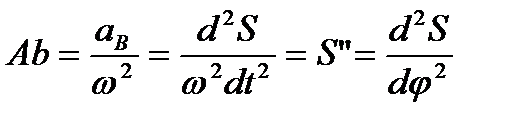Механизмы с плоским толкателем

Схема такого механизма представлена на рис. 3.1д. При работе этих механизмов угол давления в кинематической паре кулачок-толкатель всегда g = 0, поэтому заклинивание в этой кинематической паре им не грозит. Критерием же определения минимально допустимого радиуса базовой окружности кулачка является требование выпуклости профиля кулачка [14, 18], так как очевидно, что при наличии вогнутостей плоский толкатель не будет их отслеживать.

Математически условие выпуклости кулачка означает, его радиус кривизны в каждой точке должен быть положителен:

r > 0

Найдем условия, при которых это будет выполняться. Расчётные схемы показаны на рис. 3.11.

Проведем нормаль n-n в точке контакта толкателя с кулачком (рис. 3.11а). Пусть точка A является центром кривизны профиля. Как видно из рисунка

 

AB = r = R _O + s _i + A b,

 

где R_O – радиус базовой окружности кулачка, s _i – перемещение толкателя в данном положении, A b – отрезок подлежащий определению.

Заменим высшую кинематическую пару кулачок-толкатель на две низших, добавив фиктивное звено AB, как это показано на рис. 3.11б. При этом получаем кулисный механизм. Построим для него план ускорений, соответствующий векторному уравнению:

 

где a _B – ускорение толкателя, a _B= w_К S” = d²S/dt² ,

a _Aⁿ = w_К² r – нормальное ускорение точки A кулачка (r = OA),

a _BO^t – тангенциальное ускорение относительного движения (параллельно xx).

Построенный на плане механизма треугольник OAb подобен плану ускорений с полюсом в точке A. Следовательно, беря отношения соответствующих сторон, найдем:

Откуда искомый отрезок

где j – угол поворота кулачка, S” – аналог ускорения толкателя, по своему физическому смыслу это ускорение толкателя при единичной угловой скорости кулачка.

Таким образом, радиус кривизны кулачка

r = R _O + s _i + S”.

И условие выпуклости кулачка:

r = R _O + s _i + S” ³ 0. (3.12)

Поскольку R_O и s _i всегда положительны, то радиус кривизны может изменить знак только в том случае, если отрицательное значение аналога ускорения S” станет по абсолютной величине больше суммы R_O + s _i. Беря предельный случай, получаем, что условие выпуклости будет выполнено, если

 

R _O ³ – (s _i + S”) = – [s _i (j) + S”(j)] (3.13)

 

Эта формула показывает, что наименьший допустимый радиус базовой окружности кулачка R_Omin определяется величинами перемещения толкателя s и аналога ускорения S”; решение надо искать в отрицательной зоне графика S”(j), для тех положений толкателя, в которых отрицательное значение S” по абсолютной величине больше положительных значений s.

На рис. 3.11в показана диаграмма, с помощью которой можно найти величину R_O, такую, что профиль кулачка будет выпуклым. Здесь строится график функции S”(s), в одном масштабе по вертикальной оси откладывается перемещение s толкателя, а по горизонтальной – S”; это векторная величина, направление которой получают, повернув вектор скорости толкателя на 90^O в сторону, противоположную вращению кулачка.

Преобразуем неравенство (3.13):

R_O + s _i ³ –S”

или 1 ³ S”/(R _O + s _i)

tg 45^O ³ S”/(R _O + s _i)

Проведем к отрицательной ветви кривой S”(s) касательную t-t под углом 45^О к оси S. Значение минимально допустимого радиуса базовой окружности кулачка определится выражением:

R _{o min} = (S”_D/tg 45^o) – S_D; (3.14)

где: S_D, S”_D – значения перемещения толкателя и аналога его ускорения, соответствующие точке D, в которой t-t касается S”(s).

На практике R_o вбирают несколько большим, чем R_{o min} .