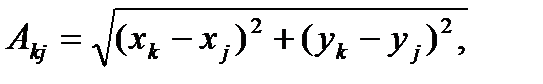Механизмы с коромыслом и роликом

(3.37)

Расчетная схема для построения профиля кулачка механизма данного типа методом инверсии представлена на рис. 3.19. Здесь, как и для механизма с толкателем, расчет профиля кулачка начинается с построения его центрового профиля Ц, т.е. траектории точки A в обращенном движении. Полярные координаты центрового профиля (R _i, b _i) относительно оси X’ для i -го положения (j = j _i) вычисляются по формулам [5, 9][4]:

где y _i – угол поворота коромысла O₁A в положении;

y₀ = arccos[(L ² + l _к² – R ₀²) / (2 L l _к)] – угол, характеризующий начальное положение коромысла;

g₀ = arccos[(R ₀² + L ² – l _к²) / (2 R ₀ l _к)];

g _i = arccos[(R_i ² + L ² – l _к²) / (2 R_i l _к)].

При расчете угла b _i знак плюс берется, если на фазе удаления направления вращения кулачка и коромысла противоположны (см. рис. 3.19), и знак минус – если одинаковы. Произведя расчеты по формулам (3.37) для i = 1, 2,... n, получаем координаты центрового профиля кулачка для всего профилируемого участка.

Радиус-вектор R_1i рабочего профиля P ₁ определяется из треугольника OA _i B по теореме косинусов:

 

(3.38)

 

 

где R_P – радиус ролика.

Полярный угол, для которого вычислен R_1i в обращенном движении:

(3.39)

 

 

Для механизма с геометрическим замыканием полярные координаты точки C второго рабочего профиля P ₂ определяется из треугольника OBC по формулам (3.32), (3.33).

3.8.4. Определение радиуса ролика

При проектировании кулачкового механизма с роликом значение R_P радиуса ролика может быть задано конструктором. В этом случае необходима проверка правильности выбранной величины. Если R_P не задано, то эта величина рассчитывается на основе анализа кривизны профиля кулачка. Для неё должны удовлетворяться следующие неравенства [1, 9, 14]:

 

R_P £ 0,7 r_min; R_P £ 0,4 R _O; (3.40)

 

где r_min – минимальный радиус кривизны центрового профиля кулачка;

R _O – радиус базовой окружности кулачка.

В п. 3.8.1, 3.8.3 рассмотрен расчет координат профиля кулачка (R _i, b _i), i = 1,2 … n. По этим величинам для каждых трех точек на центровом профиле кулачка A _{i -1}, A _i, A _{i +1} (рис. 3.20) можно определить радиус описанной окружности r_i, который и будет приближенным значением радиуса кривизны центрового профиля в i -й точке.

 

x_i = R_i cos b _i; y_i = R_i sin b _i. (3.41)

 

Длины сторон треугольника A _{i -1}A _i A _{i +1}:

(3.42)

 

где k, j = i–1, i, i+1.

Решая треугольник A _{i -1}A _i A _{i +1}, получаем:

 

 

(3.43)

 

 

где p – полупериметр треугольника A _{i -1}A _i A _{i +1}.

Произведя вычисления по формулам (3.41) … (3.43) для i = 2, 3 … n-1, находим значение

r_min = min r _i.

Если R_P задан конструктором, то проверяются условия (3.40). Если он не задан или эти условия не выполняются, то конструктор, по известному теперь r_min из конструктивных соображений может принять любое значение R_P в соответствии с условиями (3.40).