Основные параметры эвольвентного зацепления

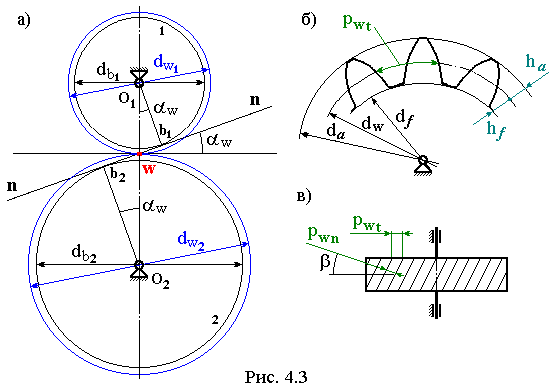
Одна из характерных окружностей зубчатого колеса фактически уже была определена – это основная окружность, диаметр которой обозначается d_b (см. рис. 4.2в) – это окружность, разверткой которой и образуется эвольвента.

На рис. 4.3а представлена схема зацепления двух колес. Окружности, проведенные из центров вращения колес через полюс зацепления, называются начальными и обозначаются d_W (все обозначения параметров стандартизованы).

При эвольвентном зацеплении требование теоремы Виллиса выполняется “с избытком”. В данном случае не только полюс зацепления неподвижен, но в процессе всего зацепления неподвижна вся общая нормаль к контактирующим поверхностям n-n. По способу образования эвольвенты очевидно, что общая нормаль является касательной к основным окружностям обоих колес и радиусы этих окружностей определяются перпендикулярами O₁b₁, O₂b₂.

Угол между касательной к начальным окружностям колес и нормалью к контактирующим поверхностям n-n называется углом зацепления a_W.

Соотношение между диаметром начальной и основной окружности:

 

d_b = d_W cos a_W (4.2)

 

Шагом зацепления называется расстояние между одноименными точками профилей двух соседних зубьев (см. рис. 4.3 б). Шаг измеряют по дуге начальной или основной окружности. В первом случае его обозначают p_W, а во втором – p_b. Для косозубых и винтовых колес шаг можно измерять по торцу зуба (см. рис. 4.3в), тогда шаг называют торцевым и в индексе ставят значок “t” или по нормали к оси зуба, в этом случае его называют нормальным и в индексе ставят значок “n”. В соответствии с выражением (4.2):

p_b = p_W cos a_W (4.3)

Нормальный шаг:

p_n = p_t cos b (4.4)

где b – угол наклона зубьев косозубого колеса (см. рис. 4.3в).

Важнейшим параметром любого зубчатого колеса является его модуль. По определению модуль зубчатого колеса это:

 

m = p_Wt / p; (4.5)

 

Подчеркнем, что выражение (4.5) – это определение понятия “ модуль зубчатого колеса ”, а не формула для его вычисления. В дальнейшем мы узнаем, что “m” определяется по условиям прочности или точности.

Понятие модуля колеса важно в первую очередь тем, что любой размер зубчатого колеса выражают в виде некоторого безразмерного коэффициента умноженного на “m”, или комбинации коэффициентов, умноженной на “m”. Это позволяет унифицировать проектные расчеты.

Величины модулей зубчатых колес стандартизованы, т.е. в ГОСТах перечислены те значения “m”, которые допускается применять при проектировании.

Теперь введем еще одну характерную окружность: так называемую делительную, её диаметр:

d = m Z; (4.6)

 

где Z – количество зубьев на колесе.

В дальнейшем, когда мы будем изучать изготовление зубчатых колес методом обкатки, будет введено понятие смещения инструмента. Сейчас предварительно отметим, что при отсутствии смещения инструмента делительная и начальная окружности совпадают.

Начальная окружность делит зуб на головку и ножку. На рис. 4.3 б обозначены: h_a – высота головки зуба, h_f – высота ножки зуба.

 

h_a = h_a^* m, h_f =(h_a^* + C^*) m (4.7)

где h_a^* – коэффициент высоты головки зуба, его значение:

h_a^* = 1 – для нормального зуба, h_a^* = 0,8 – для укороченного,

C^* – коэффициент радиального зазора, при изготовлении колеса без смещения инструмента его значение обычно принимают C^* = 0,25.

Следующие две характерные окружности зубчатого колеса: окружность выступов – её диаметр обозначается d _a и окружность впадин зубьев – d _f (см. рис. 4.3 б):

d _a = d_W + 2 h_a; d _f = d_W – 2 h_f; (4.8)

Таким образом, ножка зуба больше его головки на величину радиального зазора между окружностью выступов одного колеса и окружностью впадин – другого.