Пространственные зубчатые передачи
Пространственными называются зубчатые механизмы, позволяющие передавать вращение между валами, расположенными в различных плоскостях. К ним относятся: 1. Конические зубчатые передачи. 2. Винтовые. 3. Червячные. 4. Гипоидные. И некоторые другие. 4.7.2.1. Конические зубчатые передачи
Связь между векторами угловых скоростей
где На рис. 4.10 представлен план угловых скоростей, соответствующий векторному уравнению (4.14). Положение вектора dW1 + dW2 = S (4.15) Если вектор
Поскольку отношение угловых скоростей по определению называется передаточным отношением, то
(4.16) Для ортогональной передачи (см. рис. 4.9 б) из DOPA: R2 = OP sin dW2 из DOPB: R1 = OP sin dW1 Тогда
(4.17)
Основные параметры
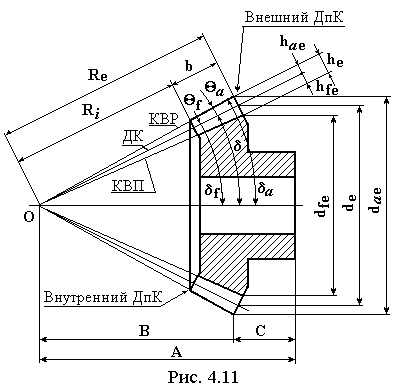
Схема конического зубчатого колеса представлена на рис. 4.11, где приняты следующие обозначения. ДК – делительный конус, КВР – конус вершин, КВП – конус впадин, Внешний и внутренний ДпК – внешний и внутренний дополнительные конусы. Все параметры колеса измеряются по внешнему ДпК, что отмечается индексом “ e ” в обозначениях параметров. 4.7.2.2. Гиперболоидные зубчатые передачи Геометрическое место положений мгновенных осей вращения называют аксоидом. В зубчатой передаче со скрещивающимися осями колес при постоянном передаточном отношении аксоидами относительного движения являются однополюсные гиперболоиды вращения. Поэтому зубчатые передачи со скрещивающимися осями колес называют гиперболоидными.
|



 и
и  звеньев 1 и 2, называют межосевым углом S.
звеньев 1 и 2, называют межосевым углом S. и
и  звеньев 1 и 2:
звеньев 1 и 2: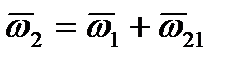 (4.14)
(4.14) – угловая скорость звена 2 относительно звена 1.
– угловая скорость звена 2 относительно звена 1.