Общий порядок силового расчета
В работах по теории механизмов показано [1, 9, 14, 18], что силовой расчет плоских рычажных механизмов удобно производить в соответствии с их структурным делением на входное звено и структурные группы (СГ) (см. главу 1). СГ отдельно взятая имеет число степеней свободы W = 0, а как доказывается в указанной литературе это является условием статической определимости кинематической цепи, то есть количество уравнений равновесия, которые мы можем составить для СГ равно количеству неизвестных реакций, которые надо определить. Поэтому эти ситемы уравнений равновесия легко решаются. Общий порядок силового расчета следующий. Начинается он с последней структурной группы, для неё: 1. Вычисляются все внешние силы, приложенные к её звеньям. 2. Для каждого звена внешние силы приводятся к главному вектору и главному моменту. 3. Составляются и решаются уравнения равновесия, в результате чего получают искомые реакции в кинематических парах данной группы. 4. Реакция в той кинематической паре, которой данная группа присоединяется к предыдущей, взятая с обратным знаком будет внешней силой для предыдущей структурной группы.
Проиллюстрируем общий порядок силового расчета на примере шестизвенного механизма, представленного на рис. 5.1а. 1. Производится расчет структурной группы А2-В2-С2 (рис. 5.1б). а) Внешняя нагрузка: б) В результате решения уравнений равновесия для данной структурной группы определяем реакции в шарнире А2 – 2. Производится расчет структурной группы А1-В1-С1 (рис. 5.1в). а) Внешняя нагрузка: б) В результате решения уравнений равновесия для данной структурной группы определяем реакции в шарнирах А1 – 3. Внешней нагрузкой для силового расчета кривошипа 1 (рис. 5.1г) будет реакция в шарнире А1 со стороны 2-го звена на 1-е, найденная на предыдущем шаге В данном примере для наглядности рассмотрен сравнительно простой механизм, образованный последовательным присоединением двух структурных групп ко входному звену, характерный для курсовых проектов по ТММ. Программа Mechanic позволяют исследовать механизмы, имеющие параллельные ветви, когда ко входному звену присоединяется несколько структурных групп. В этом случае надо просчитать каждую из них и на входное звено будут действовать реакции от всех ветвей. Это же относится и к структурным группам. Если к какой-то из них присоединяется несколько других групп, то реакция от каждой будет внешней силой для расчета данной структурной группы.
|


 – главный вектор сил, действующих на ползун 5, представляющий собой в данном случае алгебраическую сумму технологической силы, силы инерции и тяжести;
– главный вектор сил, действующих на ползун 5, представляющий собой в данном случае алгебраическую сумму технологической силы, силы инерции и тяжести; 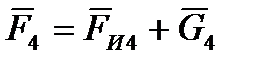 – главный вектор сил инерции и тяжести, действующих на шатун 4, M4 = MИ4 – главный момент сил инерции, действующих на шатун 4.
– главный вектор сил инерции и тяжести, действующих на шатун 4, M4 = MИ4 – главный момент сил инерции, действующих на шатун 4.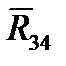 , в шарнире В2 –
, в шарнире В2 –  и в направляющих ползуна С2 –
и в направляющих ползуна С2 –  .
.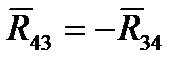 найденная на предыдущем шаге реакция в шарнире А2 со стороны 4-го звена на 3-е,
найденная на предыдущем шаге реакция в шарнире А2 со стороны 4-го звена на 3-е,  , M2 = MИ2,
, M2 = MИ2, 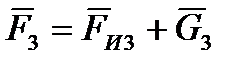 , M3 = MИ2 – главные векторы и главные моменты сил инерции и тяжести, действующих соответственно на шатун 2 и коромысло 3.
, M3 = MИ2 – главные векторы и главные моменты сил инерции и тяжести, действующих соответственно на шатун 2 и коромысло 3. , В1 –
, В1 –  , С1 –
, С1 –  .
. . Решением уравнений равновесия кривошипа определяем реакции в его опоре О –
. Решением уравнений равновесия кривошипа определяем реакции в его опоре О –  .
.


