Определение реакций в кинематических парах структурных групп
В соответствии с общим порядком силового анализа, описанным в п. 5.2 после расчета внешних сил составляют уравнения равновесия структурных групп, решением которых и определяются искомые реакции. Изображения структурных групп здесь будут упрощенными, т.к. при формировании уравнений равновесия в общем виде мы будем оперировать значениями координат кинематических пар и точек приложения сил. Эти величины определяются методами кинематики, рассмотренными в гл. 2 и здесь важна не конфигурация звеньев, а знание расположения этих точек. 5.4.1. Аналитическое решение При составлении уравнений равновесия будем предполагать, что все внешние силы, действующие на каждое i -е звено приведены к главному вектору Fi, приложенному в центре масс S i и главному моменту Mi. Индексация реакций: Rij – реакция со стороны i -го звена на j -е. Индексация звеньев принята такой же, как при кинематическом анализе в главе 2, звенья структурных групп имеют номера 2 и 3; звено 1 – то, с которым звено 2 образует кинематическую пару “A”; звено 4 – то, с которым звено 3 образует кинематическую пару “C”. Обратите внимание, для трехшарнирной и кулисных структурных групп решение будет получено сразу в НСК ОX0Y0, а для остальных – в НСК ОXY, повернутой так, чтобы ось X была параллельна выходному ползуну. Это связано с тем, что для этих групп уравнения равновесия в такой системе координат записываются и решаются намного проще, чем в НСК ОX0Y0, ну а преобразовать результаты из одной НСК в другую не составляет труда. 5.4.1.1. Трёхшарнирная структурная группа
Уравнение равновесия структурной группы в целом в виде равенства нулю суммы всех сил, на нее действующих:
R12y + F2y + F3y + R43y = 0. Равновесие шатуна 2 в виде равенства нулю суммы моментов всех сил относительно точки В: –R12x (yA – yB) + R12y (xA – xB) – F2x (yS2 – yB) + F2y (xS2 – xB) = 0. (5.5) Равновесие звена 3 в виде равенства нулю суммы моментов всех сил относительно точки В: –R43x (yС – yB) + R43y (xС – xB) – F3x (yS3 – yB) + F3y (xS3 – xB) = 0. (5.6) Уравнения (5.4), (5.5), (5.6) образуют линейную алгебраическую систему относительно неизвестных R12x, R12y, R43x, R43y, которая легко решается. Для определения реакции R23 в шарнире B теперь достаточно рассмотреть, равновесие звена 3:
R23y = – F3y – R43y. Полные величины реакций:
5.4.1.2. Структурная группа "шатун – ползун"; Расчетная схема для структурной группы данного вида представлена на рис. 5.5. Реакции в направляющих ползуна зависят от его конструкции. Имеется два основных случая: 1. Реакции перемещаются по направляющим вместе с ползуном. В этом случае рабочие длины l 1, l 2 являются конструктивными параметрами (см. рис. 5.5а, 5.5в).
Но в обоих случаях величины l 1, l 2 для силового расчета можно считать известными. В данном случае решение удобно получить в НСК OXY, ось X которой параллельна оси ползуна. Уравнение равновесия структурной группы в целом в виде равенства нулю суммы всех сил, а нее действующих:
R12y + F2y + F3y + R43 (1) + R43 (2) = 0.
Из первого уравнения системы (3.8) сразу определяется составляющая R12x. Равновесие шатуна 2 в виде равенства нулю суммы моментов всех сил относительно точки В: –R12x (y A – y B) + R12y (x A – x B) – F2x (y S2 – y B) + F2y (x S2 – x B) = 0. (5.9) Отсюда находим R12y. Для определения реакций R43(1), R43(2) составим систему уравнений, первое из которых отражает равновесие ползуна 3 в виде равенства нулю суммы проекций всех сил на ось Y, а второе – равенство нулю суммы моментов всех сил относительно точки В:
–R43(1) l 1 + R43(2) l 2 – F3x (y S3 – y B) + F3y (x S3 – x B) = 0. Длины l 1, l 2 надо подставлять с учетом знака, на рис. 5.5 показаны направления, которые считаются положительными. Для определения реакции R32 в шарнире В достаточно рассмотреть, равновесие шатуна 2 в виде равенства нулю суммы всех сил, на него действующих:
R32y = – F2y – R12y.
5.4.1.3. Кулисные структурные группы
Для определения реакций применим следующий прием. Сначала для ползуна “B” найдем не реальные реакции R23(1), R23(2) (см. рис. 5.7) а условные, приведенные к центру ползуна: реакцию R23п и соответствующий реактивный момент M23п. Запишем условия равновесия звена 2 в виде равенства нулю суммы моментов относительно точки “А” всех сил, на него действующих и равновесия кулисы 3 в виде равенства нулю суммы моментов всех сил относительно точки “С” и учитывая, что R23п = – R32п, M23п = – M32п
–F3x (y S3 – y С) + F3y (x S3 – x С) + M3 + M23п ± R23п l BD = 0, где: l 21 – смещение шарнира “А” вдоль оси кулисы, l BD – длина вектора, определяющего положение ползуна на кулисе. Из системы (5.12) определяем R23п, M23 п. Равновесие звена 2 в виде равенства нулю суммы всех сил, на него действующих:
R12y + F2y + F3y + R23п cos j3 = 0, где: j3 – угол, определяющий положение оси кулисы (см. рис. 2.11). Из системы (5.13) находим R12x , R12y. Равновесие структурной группы в целом в виде равенства нулю суммы всех сил, на нее действующих:
R12y + F2y + F3y + R43y = 0.
Теперь по значениям R32п, M32п при известных размерах ползуна l 1, l 2 (рис. 5.7) не сложно найти величины реальных реакций в ползуне “В” R32(1), R32(2) из следующей системы уравнений:
– R32 (1) l 1 + R32 (2) l 2 = M32 п.
Условия равновесия звена 2 в виде равенства нулю суммы моментов относительно точки “А” и равновесия звена 3 в виде равенства нулю суммы моментов всех сил относительно точки “С”:
–F3x (y S3 – y С) + F3y (x S3 – x С) + M3 + M23п ± R23п l AB = 0. где: l 21 – смещение шарнира “А” вдоль оси звена 3, l AB – длина вектора, определяющего положение ползуна. Из системы (5.16) определяем R23п, M23 п.
Равновесие звена 2 в виде равенства нулю суммы сил, на него действующих:
R42y + F2y + F3y + R23п cos j3 = 0. где: j3 – угол, определяющий положение оси звена 3 (см. рис. 2.12). Из системы (5.17) находим R42x, R42y. Равновесие структурной группы в целом в виде равенства нулю суммы всех сил, на нее действующих в проекциях на оси НСК OX0Y0:
R42y + F2y + F3y + R13y = 0. Отсюда находим R13x, R13y. После чего из уравнений вида (5.15) получаем реальные реакции в ползуне “В” R32(1), R32(2). 5.4.1.4. Структурная группа типа "шарнир – ползун – ползун";
Для определения реакций в ползуне “B” применим прием, описанный в п. 5.4.1.3 для кулисных структурных групп. Сначала для ползуна “B” найдем условные реакции, приведенные к центру ползуна: R32п и соответствующий реактивный момент M32п. Решение удобно получить в НСК OXY, ось X которой параллельна оси ползуна “С”. Уравнение равновесия структурной группы в виде равенства нулю суммы проекций всех сил, на ось X: R12x + F2x + F3x = 0; (5.19) отсюда сразу определяется составляющая R12x. Условия равновесия звена 2 в виде равенства нулю суммы всех сил, на него действующих:
R12y + F2y – R32п cos d = 0,
где: d – угол между осями ползунов (см. рис. 5.9). Из системы (5.20) находим R32п, R12y. Условия равновесия звена 2 в виде равенства нулю суммы моментов всех сил относительно центра ползуна “В” позволяет определить M32п :
–R12x (y A – y B) + R12y (x A – x B) – F3x (y S3 – y B) + F3y (x S3 – x B) + M32п = 0 (5.21)
И, наконец, из системы (5.22), образованной условиями равновесия структурной группы в виде равенства нулю суммы проекций всех сил, на ось Y и суммы моментов относительно центра ползуна “С” находим реакции в ползуне “С” R43(1), R43(2). R12y + F2y + F3y + R43(1) + R43(2) = 0, –R12x (y A – y С) + R12y (x A – x С) – F2x (y S2 – y С) + F2y (x S2 – x С) + M2 – – F3x (y S3 – y С) + F3y(x S3 – x С) + M3 + R43(1) l 1 + R43(2) l 2 = 0. (5.22)
Реальные реакции в ползуне “В” R32(1), R32(2) получаем из уравнений вида (5.15). 5.4.1.5. Структурная группа "ползун – шарнир – ползун"; Расчетная схема для структурной группы данного вида представлена на рис. 5.10. Реакции в направляющих ползунов зависят от их конструкции, возможные варианты описаны в п. 5.4.1.2.
В данном случае решение удобно получить в НСК OXY, ось X которой параллельна оси ползуна “С”. Уравнение равновесия звена 3 в виде равенства нулю суммы проекций всех сил, на ось X дает составляющую реакции в шарнире “В”: R23x = –F3x. Система (5.24), составленная из условий равновесия звена 2 позволяет определить R23y, R12п, M12п. –R12п sin j2+ F2x + R23x = 0, R12п cos j2+ F2y + R23y = 0, (5.24) ±R12п l BD + M12п – F2x (y S2 – y B) + F2y (x S2 – x B) = 0.
Из системы (5.26), образованной условиями равновесия звена 3 в виде равенства нулю суммы проекций всех сил, на ось Y и суммы моментов относительно центра ползуна “С” находим реакции в ползуне “С” R43(1), R43(2). R23y + F3y + R43(1) + R43(2) = 0, –R23x (y B – y С) + R23y (x B – x С) – F3x (y S3 – y С) + F3y(x S3 – x С) + M3 + + R43(1) l 1 + R43(2) l 2 = 0, (5.26) Реальные реакции в ползуне “A” R12(1), R12(2) получаем из уравнений вида (5.15). 5.4.2. Графо-аналитическое решение задачи силового расчёта Рассмотрим случай, характерный для курсовых проектов, когда силы тяжести и инерции пренебрежимо малы по сравнению с усилием R43. Расчетная схема представлена на рис. 5.11а. Реакция R34 была найдена при расчете предыдущей структурной группы и
Уравнение равновесия всей структурной группы в целом:
Здесь четыре неизвестных Равновесие звена 2 в виде равенства нулю суммы всех моментов относительно точки B1: R12t× l AB = 0 показывает, что при принятых допущениях R12t = 0. Равновесие звена 3 в виде равенства нулю суммы всех моментов относительно точки B1: R63t× l BC + R43×h43 = 0 позволяет определить величину R63t. Длину плеча h43 можно замерить на выполненной в масштабе расчетной схеме. Теперь уравнение равновесия (5.27) можно решить графически путем построения плана сил (см. рис. 5.11б). План сил представляет собой графическое изображение уравнения равновесия. Сначала в выбранном масштабе KF отложите известные силы R43 и R63t. Потом замкните план, проведя линии действия R63n и R12n. Примечание. Силовой расчет этой структурной группы рассмотрен на примере схемы 3 главного механизма шестизвенного пресса. Для схемы 1, в которой совпадают точки B1 и A2 R63t = 0 и план сил упрощается до треугольника. В схеме 2 точки B1 и A2 не совпадают, но расположены иначе, R63t ¹ 0 и все выкладки аналогичны, но план сил имеет несколько другую конфигурацию.
|






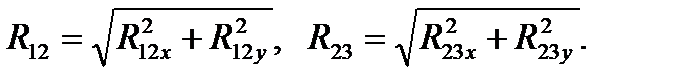 Полные величины реакций:
Полные величины реакций: Расчетная схема кулисной структурной группы первого вида представлена на рис. 5.6.
Расчетная схема кулисной структурной группы первого вида представлена на рис. 5.6.
 Отсюда находим R43x, R43y.
Отсюда находим R43x, R43y.


 .
.
 (5.27)
(5.27) . Касательные составляющие найдем, рассматривая равновесия отдельных звеньев.
. Касательные составляющие найдем, рассматривая равновесия отдельных звеньев.


