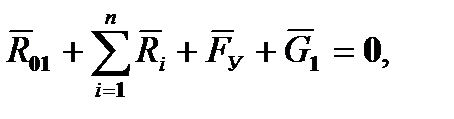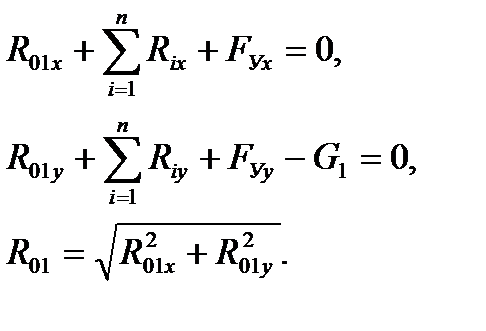Двухколенный кривошип
Наиболее часто встречающийся в курсовых проектах по ТММ случай, когда к кривошипу присоединяется несколько структурных групп – это коленчатый вал, приводящий в движение несколько шатунно-ползунных групп. На рис. 5.15 представлен пример такого механизма с двумя группами. Задача в данном случае состоит в определении реакций в опорах кривошипа.
5.5.2.1. Крутящий момент на кривошип передаётся через зубчатую или фрикционную пару
Уравновешивающая сила определяется из условия равновесия моментов всех сил, действующих на кривошип:
(5.30)
где: h i – плечи, на которых соответствующие силы создают крутящие моменты, на рис. 5.17а показаны плечи h2 и hу, n – количество структурных групп, присоединенных к кривошипу. Если момент передается через зубчатую пару, то aw (см. рис. 5.17а) это угол зацепления, а если через фрикционную – то aw = 0. Если силовой расчет производится после динамического исследования характера движения кривошипа (см. гл. 7), то при вычислении уравновешивающей силы появляется возможность учесть и инерционную нагрузку:
где: MИ = J пр e1 – инерционный момент, действующий на кривошип в данном положении, J пр – значение приведенного момента инерции машины, e1 – угловое ускорение кривошипа. Реакцию R01 в опоре кривошипа найдем из условия равновесия в виде равенства нулю суммы всех сил, действующих на кривошип:
(5.32) где: G 1 – вес кривошипа. Уравнение (5.32) можно решить графически, построив план сил (рис. 5.17б), или аналитически, составив систему уравнений равновесия спроецировав векторное уравнение (5.32) на оси НСК X0Y0, тогда:
(5.33)
Характерными особенностями данного варианта являются: 1. Уравновешивающая сила создает дополнительную составляющую реакции в опоре кривошипа. 2. Величина этой дополнительной составляющей зависит от характера внешних сил, диаметра колеса 1 на валу кривошипа и расположения шестерни 2 относительно колеса 1. 5.5.2.2. Крутящий момент на кривошип передается через планетарный или волновой механизм Схема в аксонометрии показана на рис. 5.16. Соответствующая плоская расчетная схема представлена на рис. 5.18а.
(5.34)
где: h i – плечи, на которых силы R i создают крутящие моменты, nСГ – количество структурных групп, присоединенных к кривошипу. Слагаемое “MИ” поставлено в скобках т.к. оно учитывается или нет в зависимости от стадии, на которой производится силовой расчет (см. комментарии к уравнениям 5.30). Реакцию R01 в опоре кривошипа найдем из условия равновесия в виде равенства нулю суммы всех сил, действующих на кривошип:
(5.35) где: G 1 – вес кривошипа. Уравнение (5.35) можно решить графически, построив план сил (рис. 5.18б), или аналитически, составив систему уравнений равновесия спроецировав векторное уравнение (5.35) на оси НСК X0Y0, тогда:
(5.36)
Характерной особенностью данного варианта является то, что в опоре кривошипа не возникает дополнительных составляющих реакции, что можно отнести к достоинствам планетарных и волновых механизмов.
|

 В общем случае к входному механизму (ВМ) может присоединяться несколько структурных групп. После определения реакций в их кинематических парах становятся известными усилия R1, R2,... Rn, действующие на ВМ со стороны рычажного механизма. В общем случае эти усилия могут быть приложены в произвольных точках ВМ. Ниже силовой расчет иллюстрируется конкретными примерами, но результаты будут получены в общем виде.
В общем случае к входному механизму (ВМ) может присоединяться несколько структурных групп. После определения реакций в их кинематических парах становятся известными усилия R1, R2,... Rn, действующие на ВМ со стороны рычажного механизма. В общем случае эти усилия могут быть приложены в произвольных точках ВМ. Ниже силовой расчет иллюстрируется конкретными примерами, но результаты будут получены в общем виде.

 .
.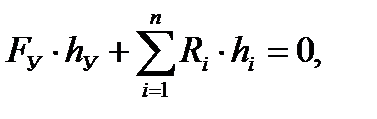
 (5.31)
(5.31)