Неуравновешенных масс
Данная задача обычно возникает на этапе испытаний и доводки уже изготовленного ротора. Поскольку ротор спроектирован уравновешенным, то фактическая неуравновешенность после его изготовления может быть вызвана следующими причинами: 1. Неизбежные погрешности изготовления деталей и их сборки. 2. При сложной конструкции ротора возможны ситуации, когда не удается точно рассчитать положение центров масс. В результате расчеты, описанные в п. 6.2.1. не дают точных результатов. 3. Неравномерная плотность материала, в частности дефекты, например, литейные раковины. Перечисленные факторы носят случайный характер. Еще раз проиллюстрируем физический смысл статической и моментной неуравновешеннности. На рис. 6.3а изображен ротор, который спроектирован как уравновешенный, но по указанным причинам его центр масс – точка S смещен относительно оси вращения, т.е. фактически ротор статически не уравновешен и сила инерции FИ вызывает появление дополнительных реакций R1, R2. Рис. 6.3б иллюстрирует моментную неуравновешенность. Этот ротор может быть статически и уравновешен, но имеет прекос. Точка S1 – это центр масс части ротора, расположенной выше оси вращения, S2 – центр масс части ротора, расположенной ниже оси вращения. Если ротор статически уравновешен, то силы инерции FИ1, FИ2 равны по величине, но они создают момент на плече h, который вызывает появление дополнительных реакций R3, R4. Поскольку, как уже отмечалось, факторы, вызывающие наличие остаточного дисбаланса, носят случайный характер, то невозможно создать методики расчёта противовесов подобные тем, что описаны в п. 6.2.1. Здесь параметры противовесов надо определять на базе результатов экспериментов с ротором.
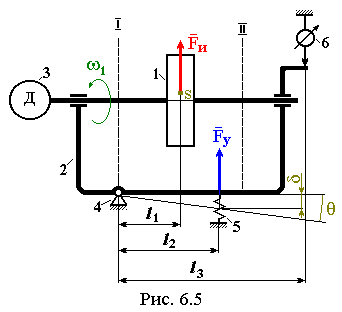
Статическое уравновешивание. Простейшие схемы статического уравновешивания ротора представлены на рис. 6.4, где 1 – ротор, 2 – призмы, 3 – свободно вращающиеся опоры. Ротор укладывают на призмы или вращающиеся опоры так, чтобы он мог свободно вращаться. Если после установки ротор самопроизвольно поворачивается – то, значит, его центр масс смещен с оси вращения и после поворота он, очевидно, находится на вертикальной оси ниже конструктивного центра. Следует или удалить часть материала на нижней части или добавить какую-то массу в верхней части. Эти операции повторяют до тех пор, пока при любом положении ротора перестанет наблюдаться его самопроизвольный поворот. Уравновешивание роторов на балансировочных станках. Существуют различные типы балансировочных станков. Мы рассмотрим один из вариантов. На рис. 6.5 представлена схема балансировочного станка, где 1 – ротор, 2 – рама балансировочного станка, 3 – двигатель, вращающий ротор, 4 – жесткая шарнирная опора, 5 – упругая опора, 6 – датчик, замеряющий амплитуду колебаний рамы, I и II – плоскости, в которых конструкцией ротора предусмотрена возможность постановки противовесов для уравновешивания ротора. Точка S – центр масс ротора, который может быть смещен относительно оси вращения на некоторую величину. Фактически требуется каким-то образом определить величину имеющегося остаточного дисбаланса и устранить его установкой противовесов.
1. Создать математическую модель балансировочного станка с установленным на нем уравновешиваемым ротором как механической колебательной системы. 2. Произвести эксперименты с уравновешиваемым ротором. 3. На основании данных экспериментов с помощью математической модели определить фактический дисбаланс. 4. Установить противовесы, устраняющие имеющийся дисбаланс. Для решения этой задачи будут проводиться тестовые испытания с исследованием резонансных колебаний рамы станка, поэтому сначала составим математическую модель балансировочного станка как механической колебательной системы. Создание математической модели будет состоять из следующих этапов. 1. Формирование дифференциального уравнения колебаний рамы станка под действием инерционной нагрузки от неуравновешенного ротора. 2. Нахождение его решения при резонансе. 3. Определение связи между замеряемой амплитудой колебаний, найденным решением и дисбалансом. Рама станка может колебаться вокруг жесткой шарнирной опоры 4 (см. рис. 6.5) за счет упругости опоры 5 под действием силы инерции FИ, возникающей при вращении ротора из-за наличия дисбаланса. Уравнение колебаний рамы составим, опираясь на Принцип д’Аламбера. Уравнение квазиравновесия по д’Аламберу:
MУ + MС + MВН = MИ (6.6)
где MУ – момент, создаваемый силами упругости, MС – момент, создаваемый силами сопротивления, MВН – момент, создаваемый внешними силами, MИ – момент сил инерции. Рассмотрим каждое слагаемое уравнения (6.6).
(6.7) где J – момент инерции рамы станка вместе с установленным на нем ротором и двигателем относительно оси качания рамы, q – угол поворота рамы в процессе колебаний. Внешней силой, вызывающей колебания рамы является сила инерции FИ, возникающая при вращении ротора из-за наличия дисбаланса. Момент ею создаваемый: MВН = FИ l1 sin w1t = – mK aS l1 sin w1t
где mK – неуравновешенная масса (неизвестна), aS – ускорение центра масс ротора, w1 – угловая скорость вращения ротора. Если w1 близка к постоянной, то касательной составляющей ускорения центра масс можно пренебречь и считать, что полное ускорение состоит только из нормальной составляющей aS» aSn, тогда MВН» – mK aSn l1 sin w1t = – mKw12 r K l1 sin w1t (6.8)
где rK – радиус расположения неуравновешенной массы (неизвестен). В процессе колебаний деформируется упругая опора 5, которая создает силу FУ. Момент, который при этом возникает:
MУ = FУ l2 = C d l2» C l2 2 q (6.9)
где C – коэффициент жесткости пружины, d – деформация упругой опоры.
Для момента сил сопротивления MС примем гипотезу вязкого трения, в соответствии с которой этот момент пропорционален скорости:
(6.10) где h – коэффициент демпфирования (неизвестен). Подставляя выражения (6.7) … (6.10) в уравнение (6.6) получаем:
(6.11)
или
(6.12)
Обозначим: h/J = 2n, C l 22/J = k2, mKw12 r K l1 /J = f, тогда получаем уравнение колебаний в привычном виде:
(6.13) где n – коэффициент затухания, k – собственная частота. Уравнение (6.13) и является искомой математической моделью процесса колебаний рамы балансировочного станка. Это обыкновенное линейное дифференциальное уравнения второго порядка. В дальнейшем будут использоваться результаты резонансных испытаний. Из теории колебаний известно (см., например [10, 12]), что при резонансе амплитуда колебаний такой системы:
(6.14)
Приближенное равенство в выражении (6.14) справедливо для так называемых слабо демпфированных систем, когда k >> n. Балансировочные станки конструктивно выполняются именно такими.
(6.15)
Таким образом, мы показали, что амплитуда A резонансных колебаний пропорциональна дисбалансу DK с некоторым пока неизвестным коэффициентом пропорциональности m. Для нахождения величины дисбаланса DK применим метод трех разгонов. Ротор устанавливают на балансировочный станок так, чтобы плоскость I проходила через шарнирную опору 4. Двигателем 3 ротор разгоняют в зарезонансную область, т.е. до частоты вращения w1 заведомо большей, чем k и дают выбег[5]. В процессе выбега, когда ротор медленно тормозится система проходит через резонанс w1 = k. Датчиком 6 замеряют амплитуду резонансных колебаний. Обозначим ее: A K. Далее на роторе устанавливают дополнительную, так называемую пробную массу известной величины mП. После этой операции ротор получает дисбаланс:
Производят второй разгон ротора, дают выбег и замеряют амплитуду резонансных колебаний. Обозначим ее: A 1. После этого на роторе в то же место устанавливают удвоенную пробную массу 2mП. После этой операции дисбаланс ротора:
Производят третий разгон ротора, дают выбег и замеряют амплитуду резонансных колебаний. Обозначим ее: A 2. Изобразим ситуацию графически. На рис. 6.6а представлен ротор и показан изначальный дисбаланс, характеризующийся неизвестными параметрами mK, rK и пробные массы mП, 2mП, расположенные на известном расстоянии rП.
DK2 + D22 = 2DП2 + 2D12
Тогда
(6.18)
Для уравновешивания надо в плоскости II установить противовес, имеющий дисбаланс такой же по величине, но противоположный по направлению. После этого, ротор переустанавливается так, что меняются местами плоскости I – II и все описанные операции повторяются для расчета и установки противовеса в плоскости I.
|










 В процессе экспериментов датчиком 6 (см. рис. 6.5) будет замеряться не угол поворота рамы, а амплитуда колебаний точки установки датчика:
В процессе экспериментов датчиком 6 (см. рис. 6.5) будет замеряться не угол поворота рамы, а амплитуда колебаний точки установки датчика: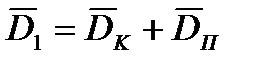 (6.16)
(6.16) (6.17)
(6.17)

 или
или




