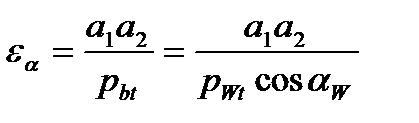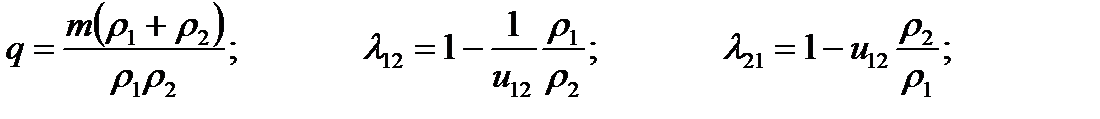Зоны одно- и двупарного зацепления, коэффициент перекрытия

Как уже отмечалось, при эвольвентном зацеплении не только полюс зацепления неподвижен, но неподвижна вся общая нормаль к контактирующим поверхностям. Следовательно, траектория точки контакта зубьев – это прямая, а точнее отрезок общей нормали. Таким образом, отрезок общей нормали, в пределах которого реально движется точка контакта, называется рабочим участком линии зацепления, а его предельно возможная величина – теоретическим участком линии зацепления.

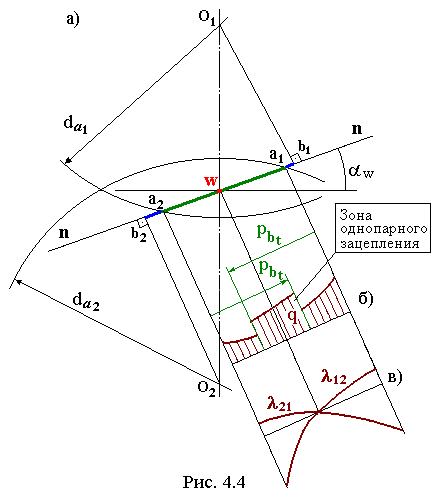
На рис. 4.4а представлено построение этих отрезков. По способу образования эвольвенты теоретический участок линии зацепления – это отрезок b₁b₂ – тот же, что и на рис. 4.3а.

Поскольку первое касание при вхождении в контакт происходит вершиной зуба, то рабочий участок линии зацепления а₁а₂ определяется пересечениями окружностей выступов с общей нормалью n-n.

(4.9))2

На рис. 4.4 б в показаны эпюры коэффициента удельного давления q и удельного скольжения l в зависимости от положения точки контакта.

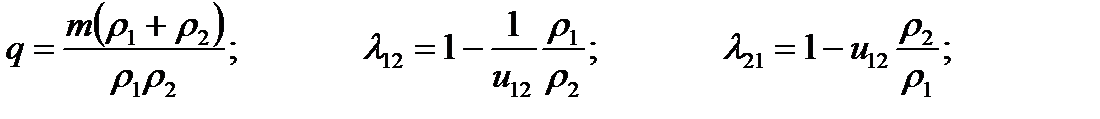
где r₁₂ – радиусы кривизны эвольвент, m – модуль зацепления, u₁₂ – передаточное число зубчатой пары.

Чтобы зацепление было плавным необходимо, чтобы до выхода из зацепления очередной пары зубьев следующая пара уже вошла в зацепление. Таким образом, в момент вхождения в зацепление очередной пары зубьев и еще некоторое время после этого в зацеплении находится две пары зубьев. Участок линии зацепления, соответствующий этому состоянию, называют зоной двупарного зацепления. Далее предыдущая пара зубьев выходит из зацепления, в зацеплении остается одна пара и вся нагрузка падает на неё. Участок линии зацепления, соответствующий этому состоянию, называют зоной однопарного зацепления. Значения удельного давления, вычисленные по формуле (4.9) соответствуют зоне однопарного зацепления, а зоне двупарного – эти величины в два раза меньше (см. рис. 4.4б).

(4.10))2

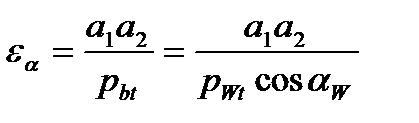
И так, в зацеплении находится попеременно то одна, то две пары зубьев. Среднее количество пар зубьев, находящихся в зацеплении называется коэффициентом перекрытия e. Для прямозубой передачи его величина равна отношению длины рабочего участка линии зацепления к шагу по основной окружности: