Метод преобразования координат

Во всех рассмотренных выше задачах выбиралась такая система координат OXY, в которой уравнения кинематики имеют наиболее простой и удобный для решения вид. Однако конечный результат часто бывает необходимо получить в некоторой неподвижной системе координат, в которой рассматривается весь механизм в целом. Кроме того, полученные в подразделе 2.3 выражения не позволяют определять кинематические параметры движения произвольных точек на звеньях механизмов, например, центров масс, рабочих органов и т.п. Все эти проблемы удобно решать методом преобразования координат.

Рассмотрим конкретный пример. Пусть требуется определить кинематическое параметры движения некоторой точки S на шатуне AB (рис. 2.15).

Суть метода. С каждым звеном механизма связывают свою систему координат. На рис. 2.15 OXY – неподвижная система координат (НСК), связанная со стойкой, AX₂Y₂ – подвижная локальная система координат (ЛСК), связанная с шатуном 2 и движущаяся вместе с ним. Координаты (.)S в ЛСК нам известны и в процессе движения они не меняются. Связь между координатами точки, измеренными в разных системах известна из аналитической геометрии, на этом и строится данный метод.

Положение начала ЛСК надо выбирать так, чтобы можно было заранее определить его кинематические параметры движения. Для рассматриваемых примеров координаты (x_A, y_A), проекции скорости (v _Ax, v _Ay) и ускорения (a _Ax, a _Ay) точки A найдём как параметры движения конца кривошипа 1 (см. п. 2.2.1).

x_A = l_ОА cos j₁,

y_A = l_ОА sin j₁,

где l_ОА – длина кривошипа.

v _Ax = – w₁ l_ОА sin j₁,

v _Ay = w₁ l_ОА cos j₁,

где w₁ – угловая скорость кривошипа.

где e₁ – угловое ускорение кривошипа.

Величины j₁, w₁, e₁ должны быть заданы по постановке задачи кинематического анализа.

Ось X₂ ЛСК следует направлять вдоль соответствующего вектора l ₂ (см. векторные контуры в п. 2.3) или параллельно ему, ось Y₂ – так, чтобы образовывалась правая система координат.

Кроме того, будем полагать, что предварительно выполнен расчёт методом векторных контуров (см. п. 2.3.1, 2.3.2), и нам известны параметры вращательного движения шатуна 2 j₂, w₂, e₂.

Координаты (.)S в НСК найдём, просто записав связь между координатами точки, измеренными в разных системах координат. В матричной форме она имеет вид:

 

(2.36)

 

Последовательно дифференцируя выражение (2.36) по времени, получим зависимости для определения проекций скорости и ускорения (.)S в НСК:

 

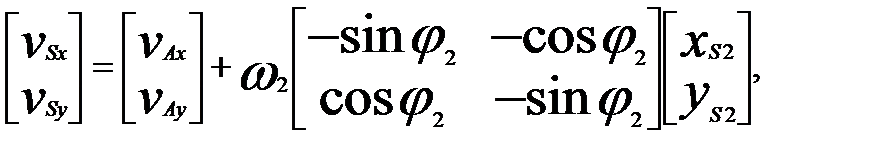
(2.37)