Структурные группы

Это понятие впервые было введено в начале 20 века русским ученым Ассуром. Поэтому структурные группы часто называют группами Ассура. По определению структурной группой называется кинематическая цепь, которая будучи своими внешними кинематическими парами установлена на стойку имеет число степеней свободы W = 0. В дальнейшем эти понятия были развиты И.И. Артоболевским, поэтому классификацию, которой далее мы будем использовать, обычно называют классификацией Ассура-Артоболевского.

По данной классификации структурной группе приписывают класс и порядок. Классом структурной группы считается количество кинематических пар во внутреннем контуре группы. Порядком – считается количество кинематических пар, которыми она присоединяется к остальному механизму. На рис. 1.4 дан пример структурной группы 3-го класса 3-го порядка. Здесь звенья 4, 5, 6 образуют внутренний контур, в котором три кинематические пары. К остальному механизму данная группа присоединяется тремя шарнирами: A, B, C.

К недостаткам данной классификации можно отнести то, что структурные группы, которым приписывается 2-й класс, 2-й порядок не имеют ярко выраженного признака второго класса. На рис. 1.5 показаны все виды таких групп.

К механизму эти группы присоединяются внешними кинематическими парами.

При структурном анализе механизма ему присваивают класс равный наивысшему классу входящей в него структурной группы. Здесь мы будем рассматривать только плоские рычажные механизмы 2-го класса 2-го порядка. Они являются наиболее простым, но широко применяемым видом рычажных механизмов. Их структура легко поддается классификации, для них удается получить аналитическое решение задачи кинематического анализа.

На рис. 1.6 дан пример структурного анализа механизма. На рис. 1.6а изображен шестизвенный, плоский рычажный механизм. Структурно он делится на входное звено – кривошип ОА (рис. 1.6 б) имеющее число степеней свободы W = 1 и две структурные группы 2-го класса, 2-го порядка (рис. 1.6 в, г).

1.4. Структурный синтез механизмов с помощью групп Ассура

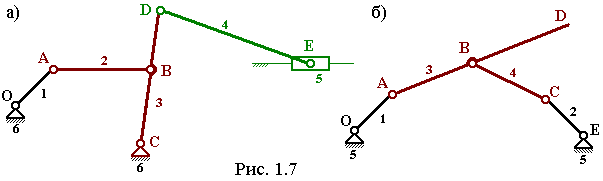
Структурный синтез механизмов с помощью структурных групп сводится к тому, что к входному механизму или к нескольким входным механизмам присоединяются структурные группы. При этом, поскольку число степеней свободы группы Ассура W = 0, то её присоединение к механизму не меняет числа степеней свободы. На рис. 1.7 приведены примеры такого синтеза. На рис. 1.7а сформирован шестизвенный механизм 2-го класса 2-го порядка, структурно состоящий из входного кривошипа 1 и двух структурных групп: ABC и DE. Поскольку у входного механизма число степеней свободы W = 1, то и у всего механизма – тоже. На рис. 1.7 б синтезирован пятизвенный механизм с числом степеней свободы W = 2. Здесь входные звенья – 1-е и 2-е, а ABC – структурная группа.

При таком синтезе созданный мехзанизм не будет иметь пассивных связей. Если при дальнейшей проработке они потребуются по соображениям прочности или жесткости, то они могут быть введены конструктивно.