Свойства пределов функцииПусть все функции, рассматриваемые ниже, определены на (а, в), кроме, быть может, фиксированной точки хо Î (а, в), тогда верны следующие свойства: 1. Если j (х) £ ¦ (х) £ y (х) и А = 2. Если ¦(х) = С (сonst) Þ 3. Если 4. Если существуют конечные пределы а) б) в) Все эти свойства доказываются одинаковым методом, основанным на соответствующих свойствах пределов последовательностей. Для доказательства этих свойств введем понятие бесконечно малых и бесконечно больших функций.
|
= 
Þ 
= A.
¦(x) = C.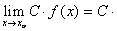
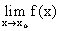, тогда:
;
;
= 
.
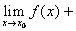
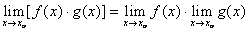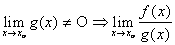