Замечание. Величина, обратная бесконечно малой, является бесконечно большой.
Величина, обратная бесконечно малой, является бесконечно большой. Пусть a = a (х), a (х) ¹ 0 при х ¹ хо есть в бесконечно малой (или бесконечно большой) тогда В дальнейшем будем использовать символические записи для любого числа а>0: Рассмотрим свойства бесконечно малых функций. 1) Алгебраическая сумма конечного числа бесконечно малых, определенная на общем множестве, есть величина бесконечно малая при х ® хо. 2) Произведение ограниченной при х ® хо функции на бесконечно малых есть функция бесконечно малая. 2") Произведение конечного числа бесконечно малого при х ® хо есть функция бесконечно малая. 3) [a(х) ]n - (n - целая положительная степень) a (х) - бесконечно малая тогда и [a (х) ]n - бесконечно малая. 4) Что касается отношения двух бесконечно малых Но с помощью действия деления можно сравнить между собой бесконечно малые. Определение 4.6. a (х), b (х) бесконечно малые при х ® хо имеют одинаковый порядок, если их отношение имеет конечный предел, отличный от нуля, т.е. Определение 4.7. Порядок бесконечно малой b (х) выше порядка бесконечно малой a(х), если отношение В этом случае пишут b(х) = 0 [a (х)] при х ® хо. Определение 4.8. Бесконечно малая b (х) имеет предел n относительно бесконечно малой a (х) при х ® хо, если Докажем одно из свойств сформулированных в1.5.3., например, свойство 4. Если существуют конечные пределы Доказательство:Пусть Тогда имеем на основании 3.2. ¦(х) = A + a (х), g(х) = B + b(х), где a(х), b(х) - бесконечно малые при х ® хо Тогда ¦(х) × g(х) = A × B + g(х), где g(х) = A × b (х) + b × a) + a (х) × b(х) - есть бесконечно малая Þ g(х) ® 0 бесконечно малая на основании свойств бесконечно малой функции. Отсюда Рассмотрим в качестве примера предел отношения синуса бесконечно малой дуги к самой дуге. Теорема 4.3. Первый замечательный предел. Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице, Доказательство: Пусть х > 0 и х ® 0, так что 0 < х <
Рис.4.4. В тригонометрическом круге R = 1 рассмотрим S DОАВ, S cек. ОАВ, SDОАВ SDОАВ = Получаем т.е. Sin x < x < tg x разделим на Sin x > 0, получим 1 < Пусть теперь х ® 0 + 0, но т.к. 1 - cos x = 2 sin2 то На основании свойства 1, получаем Если х < 0; имеем Поэтому З а м е ч а н и е. " х çsin x ç £ çx ç, причем равенство имеет место при х = 0. Теорема 4.3. Второй замечательный предел. (Число е ). Ранее было доказано, что последовательность Можно доказать, что функция у = е = Пусть где е = 2,7182818284...
|

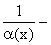 бесконечно большая (бесконечно малая).
бесконечно большая (бесконечно малая).
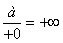 ,
, 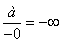 ,
, 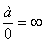 ,
, 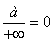 ,
,  ,
, 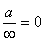 .
. ,
, 
 - может быть функция произвольного поведения.
- может быть функция произвольного поведения.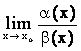 =K¹ 0.
=K¹ 0. есть бесконечно малое при х ® хо, т.е.
есть бесконечно малое при х ® хо, т.е. 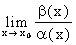 = 0.
= 0. = K ¹ 0.
= K ¹ 0. и
и 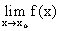 , тогда:
, тогда:
 ,
, 
 .
.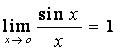 .
.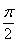 .
.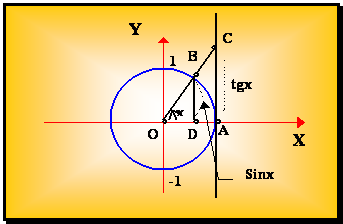
 SDОАВ =
SDОАВ = 

 или cos x <
или cos x < 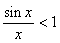 .
.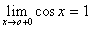
 бесконечно малая по условию,
бесконечно малая по условию, . Тогда функция
. Тогда функция  заключена между двумя функциями, имеющими предел, равный 1.
заключена между двумя функциями, имеющими предел, равный 1. .
. , где - х > 0.
, где - х > 0. .
. имеет предел, заключенный между 2 и 3.
имеет предел, заключенный между 2 и 3. , х Î (-¥, -1) È (0, +¥) при х ® ¥ стремится к е:
, х Î (-¥, -1) È (0, +¥) при х ® ¥ стремится к е: .
. , тогда e =
, тогда e = 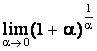 или
или  ,
,


