Рассмотрим график функции y = f(x), определенной и непрерывной на (a,b). Зафиксируем произвольную точку x на (a,b), и зададим приращение ∆ x≠ 0, причем x+∆ x є (a,b). Пусть точки M,P - точки на графике f(x), абсциссы которых равны x, x+∆ x (рис.21). Координаты точек M и P имеют вид M(x,f(x)), P(x+∆ x,f(x+∆ x). Прямую, проходящую через точки M, P графика функции f(x) будем называть секущей. Обозначим угол наклона секущей MP к оси ОX через f (∆ x).
Определение 3. Если существует предельное положение секущей MP при стремлении точки N к точке M вдоль графика функции при ∆ x → 0), то это предельное положение называется касательной к графику функции f(x) в данной точке M этого графика.
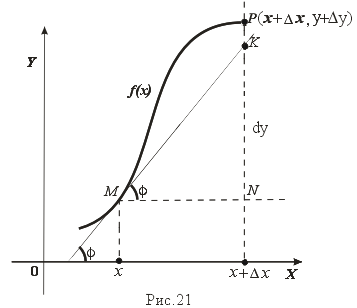
Из данного определения следует, что для существования касательной к графику f(x) в точке M достаточно, чтобы существовал предел lim∆ x → 0 φ(∆ x) = φ 0, который равен углу, образованному касательной с положительным направлением оси OX.





