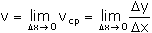Физический смысл производной
Рассмотрим, например, некоторую линейную функцию y = f(x) = ax+b. Если независимая переменная получает приращение ∆x, то функция получает приращение ∆y = a*∆x ∆y = f()-f(x) = [a*(x+∆x)+b] - [ax+b] = a*(x+∆x)+b-ax+b = a*(x+∆x)-ax = ax+a*∆x - ax = a*∆x Отношение ∆y/∆x = a*∆x/∆x = a остается постоянным, не зависящим ни от того, при каком х функция рассматривается, ни от того, какое взято ∆x. Это отношение называется скоростью изменения линейной функции. Но если функция y=f(x) не линейная, то отношение =[f(x+∆x) -f(x)]/∆x зависит и от х, и от ∆x. Это отношение только "в среднем" характеризует функцию при изменении независимой переменной от данного х до x+∆x. Определение 4. Отношение ∆y/∆x называется средней скоростью изменения функции в интервале (x, x+∆x). Ясно, что чем меньше рассматриваемый интервал, тем лучше средняя скорость характеризует изменение функции, поэтому мы должны заставить ∆x стремиться к нулю. Т.е. мы приходим к понятию производной! Скоростью изменения функции в данной точке х называется предел средней скорости изменения в интервале (x, x+∆x) при стремлении ∆x к нулю:
Последнее определение и дает нам физический смысл производной, который заключается в скорости изменения функции.
|