Точки непрерывности и точки разрыва функцииОпределение 5.1. Функция а, определенная на интервале (а, в) называется непрерывной в точке хоÎ(а, в)
Или, если ввести следующие обозначения: Dx = x0 - x, Dy = f(x) - f(x0) Dx - приращение аргумента; Dy - приращение функции. Пусть y = f(x), где х - текущая точка из области определения.
Рис.5.2. Определение 5.2. Функция f(x), определенная на Х, называется непрерывной в точке х = хо (хоÎХ). 1) функция в этой точке определена; 2) при Dх = хо - х ® 0 и, т.е. функция называется непрерывной в данной точке, если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции. f(x) - непрерывна в точке х0 Û " e>0 $ d>0: çx-x0ç<d, т.е. 0<çDx ç<d, çf(x)-f(x0)ç=çf(x0+Dx)-f(x0)½<e. Определение 5.3. Функция называется непрерывной на данном множестве Х, если
2) непрерывна в каждой точке этого множества, т.е. " х Î Х справедливо. Определение 5.4. Точка, в которой нарушается непрерывность функции, называется точкой разрыва этой функции. Пусть х0 - точка разрыва функции f и существуют конечные пределы f(x0-0)=, f(x0+0) = тогда точка х называется точкой разрыва первого рода. Величина f(x0+0) - f(x0-0) называется скачком функции f в точке х. Если f(x0-0)=f(x0+0), то х называется точкой устранимого разрыва. Если доопределить функцию таким образом, что f(x0)= Точка разрыва, не являющаяся точкой разрыва первого рода, Рис.5.3
|
Рис.5.1.
1) она определена на этом множестве, т.е. " х Î Х $ f(x);
= 
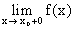, то получим непрерывную функцию.
называется точкой разрыва второго рода. Таким образом, в точках второго рода по крайней мере один из пределов не существует
.
