Бесконечно малые и бесконечно большие функции
Определение 4.4. Функция a = a(х) называется бесконечно малой функцией (или просто бесконечно малой) при х ® хo, если Лемма 4.2. Предел где a (х) - бесконечно малая. Доказательство: Пусть ¦(х) - A = a (х), получим обратно, если ¦(х) = A + a(х) и Из леммы 3.2. следует, что если Определение 4.5. Функция f = f(x) называется бесконечно большой при х ® хо, если "e > 0 $ d = d (e) > 0: ç¦(x)ç > e, "x: çx -xoç< d, x < xo. В этом случае будем писать Если "e > 0 $ d: ¦(х) > e (¦(х) < - e) "х: çх-хо ç < d, х ¹ хо Þ По аналогии с конечными односторонними пределами определяются односторонние бесконечные пределы
|
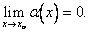
существует и равен А Û ¦ (х) = A + a (х),
, то, полагая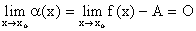
.
.
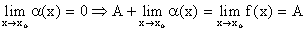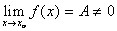, то в некоторой окрестности Охо знак f(х) (х Î C) совпадает со знаком числа А.
.
, ( 
).
, 
.
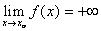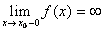