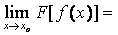Замечание. Можно, конечно, ограничиться рассмотрением левых d - окрестностей точки хо : = (хо - d, хо ) , где d = d ( e ) > 0.
Можно, конечно, ограничиться рассмотрением левых d - окрестностей точки хо: O(xо - 0, d) = { х: хо - d < x £ хо }, d > 0 O(х + 0, d) = {х: хо £ х < xo + d }, d > 0.
Рис. 4.2. Пример 4.1.
Пусть f(х) = sin х =
Здесь
Теорема 4.1. Для существования предела функции f(х) при х ® хо (хо - число) Û f(хо - о) = f(хо + о). Доказательство: Пусть тогда " e > о $ d = d(e) > о: çх -хоç< d = > çf (х) ¹ A ç < e, и следовательно $ А = Обратно, если существуют пределы А = хо - d1 < х < хо и, соответственно, хо < х < xо + d2 Þ çf(х) - Aç < e Возьмем d = min {d1, d2} Þ çf(x) - A ½< e при çх -хоç< d, х ¹ хо. И тогда, согласно определения 3.1 Лемма 4.1. Если f(х) имеет предел в точке хо, то существует окрестность этой точки (быть может, выброшенной точкой хо), на которой функция ограничена. Теорема 4.2. (Правило замены переменного для пределов функции) Пусть существуют
|
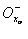= (хо - d, хо), где d = d (e) > 0.
= (xo, xo + d), где d = d (e) > 0.
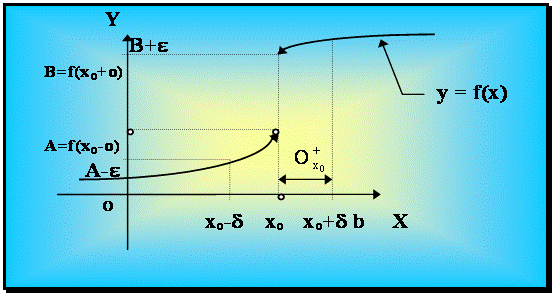
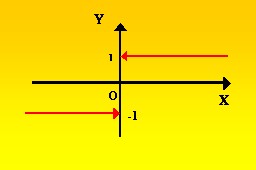Рис. 4.3.
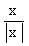,определена для всех x ¹ 0.
, а 
.
,
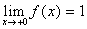= (хо - d, хо) и 
= (xо, xо + d):
и А = 
.
f(x) и А =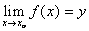 
o, f(х) ¹ уо " х ¹ хо и 
Þ при х ® хо существует предел сложной функции F[f(x)] и 
