МЕТОДЫ МОЛЕКУЛЯРНОЙ БИОЛОГИИ.

ИСТОРИЯ ИЗУЧЕНИЯ НУКЛЕИНОВЫХ КИСЛОТ.

 

 

ПЛАН:

 

1. Молекулярная биология как наука. Возникновение.

2. Задачи молекулярной биологии.

3. Основополагающие открытия молекулярной биологии. Основной постулат.

4. Взаимосвязь молекулярной биологии с другими науками.

5. Возникновение новых наук – геномики и протеомики. Создание банков генов.

6. Методы молекулярной биологии: - микроскопия;

- рентгеноструктурный анализ;

- использование радиоактивных изотопов;

- ультрацентрифугирование;

- хроматография;

- электрофорез;

- изоэлектрофокусирование;

- метод культуры клеток;

- бесклеточные системы;

- моноклональные антитела и др.

 

____________________________

 

 

«Молекулярная биология изучает связь структуры биологических макромолекул и основных клеточных компонентов с их функцией, а также основные принципы и механизмы саморегуляции клеток, которые опосредуют согласованность и единство всех протекающих в клетке процессов, составляющих сущность жизни» - Дж. Уотсон, 1968 г.

 

Задачи молекулярной биологии:

 

ü расшифровка структуры геномов;

ü создание банков генов;

ü геномная дактилоскопия;

ü изучение молекулярных основ эволюции, дифференцировки, биоразнообразия, развития и старения, канцерогенеза, иммунитета и др.;

ü создание методов диагностики и лечения генетических болезней, вирусных заболеваний;

ü создание новых биотехнологий производства пищевых продуктов и разнообразных биологически активных соединений (гормонов, антигормонов, релизинг-факторов, энергоносителей и др.)

 

 

Этапы:

1) Ф. Мишер (F. Miesher) впервые выделил ДНК (1869г.); А.Н. Белозерский

выделил ДНК из растений.

2) 50-е годы XX века - получены данные об элементарном строении белков и нуклеиновых кислот.

3) 60-е - 70-е гг. XX века – раскрыта природа и основные пути передачи и реализации генетической информации. Сформулирован основной постулат.

4) 70-е - 80-е гг. XX века – изучение механизмов сплайсинга, открытие РНК-ферментов и аутосплайсинга, изучение механизмов генетической рекомбинации, начинаются работы по расшифровке структуры геномов высших организмов, возникает белковая инженерия; организация банков генов.

5) 90-е гг. XX века – начало XXI века – развитие биоинформатики; определение нуклеотидных последовательностей (секвенирование) ДНК различных организмов: 1995г. – секвенирован первый бактериальный геном, 1997г. – геном дрожжей, 1998г. – геном нематоды, 2000г. – геном дрозофилы, 2001г. – почти полностью геном человека.

 

 

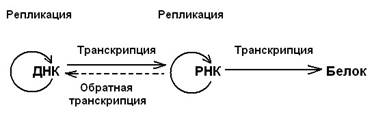
В середине 60-х гг. XX века окончательно сформирован основной постулат молекулярной генетики, формулирующий магистральный путь реализации генетической информации в клетке: ДНК → РНК → белок

И был дополнен представлениями о существовании процесса обратной транскрипции (о биосинтезе ДНК на матрице РНК) и репликации РНК:

 

Заполните таблицу:

 

Год	Ученый(е)	Открытие(я)

 

Постепенно молекулярная биология становится в центре наук, составляющих современную физико-химическую биологию:

 

 

 

 

 

В начале 80-х годов XX века возникла новая наука – биоинформатика – на стыке молекулярной генетики и информатики. В 1982 г. были организованы банки нуклеотидных последовательностей: Gen Bank в США и EMBL в Европе, в которых концентрировалась информация о расшифрованных нуклеотидных последовательностях ДНК различных организмов. Прогресс в области определения нуклеотидных последовательностей ДНК различных организмов привел к возникновению геномики – науки, изучающей наборы всех генов данного организмов как единое целое. Одновременно возникла протеомика – наука, исследующая полные наборы белков, функционирующих на различных этапах развития того или иного организма.