Лабораторна робота № 23
ВИЗНАЧЕННЯ КОЕФІЦІЄНТА ПОВЕРХНЕВОГО НАТЯГУ РІДИНИ МЕТОДОМ ВІДРИВУ КРАПЛІ Мета роботи:Визначити коефіцієнт поверхневого натягу невідомої рідини. Обладнання:бюретка, досліджувана рідина.
Теоретичні відомості Рідини за своїми властивостями займають проміжне місце між газами та твердими тілами і мають ознаки як газу, так і кристалічного тіла. Зокрема, для рідин, як і для кристалів, характерна наявність певного об’єму, і водночас рідини, як і гази, займають форму посудини, в якій вони знаходяться. Для кристалічних тіл характерно впорядковане розміщення частинок (дальній порядок). За даними рентгенографічних досліджень в рідинах спостерігається ближній порядок (впорядковане розміщення сусідніх частинок довкола даної на незначних віддалях). У зв’язку з відсутністю в рідинах дальнього порядку в них не виявлено анізотропії (залежності фізичних властивостей від напряму), характерної для кристалів. У рідинах, з видовженими молекулами, спостерігається однакова орієнтація молекул у межах певного об’єму. В таких рідинах має місце анізотропія оптичних і інших властивостей. Рідини з такими властивостями одержали назву рідких кристалів. Тепловий рух молекул має такий характер: молекула протягом певного часу коливається відносно тимчасового положення рівноваги, а потім стрибком переміщується в нове положення рівноваги. З підвищенням температури амплітуда і частота стрибків збільшуються.
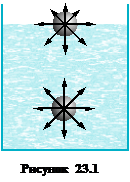
Ці молекулярні сили треба враховувати до певної відстані між молекулами, яка має назву радіуса молекулярної взаємодії. Кожна молекула в середині рідини (рис. 23.1) зазнає притягання з боку всіх тих молекул, які знаходяться в сфері радіуса молекулярної взаємодії r, центр якої співпадає з центром даної молекули. Рівнодійна всіх сил, в даному випадку, дорівнює нулю. Якщо ж молекула знаходиться на поверхні рідини або на відстані від поверхні, яка менша радіуса молекулярної взаємодії, то рівнодійна всіх сил не дорівнює нулю і напрямлена усередину рідини. При переході молекули з глибини рідини в поверхневий шар над молекулою виконується від’ємна робота і молекула набуває потенціальної енергії. Таким чином, молекули в поверхневому шарі мають додаткову потенціальну енергію, величина якої пропорційна площі поверхні, тобто
де З рівняння (23.1) коефіцієнт поверхневого натягу
В системі SI коефіцієнт поверхневого натягу вимірюється в Коефіцієнт поверхневого натягу можна виразити і так:
тобто, як відношення сили поверхневого натягу до довжини межі поверхні, на яку діє ця сила. Поверхневий натяг суттєво залежить від температури, так як з підвищенням температури збільшується віддаль між молекулами, а значить зменшуються сили взаємодії.
Поверхневий натяг залежить і від домішок, які є в рідині. Речовини, які послаблюють поверхневий натяг рідини, називаються поверхнево – активними речовинами (наприклад, по відношенню до води - мило). Є речовини, які збільшують поверхневий натяг води – цукор, сіль та інші. Збільшення чи зменшення поверхневого натягу пояснюється величиною сил взаємодії між молекулами рідини і молекулами рідини та домішок. Є різні методи визначення коефіцієнта поверхневого натягу: метод відриву краплі, відриву кільця, метод Ребіндера, метод підняття чи опускання рідини в капілярних трубках і ін.. Коли рідина витікає з капіляра, то на кінці капіляра утворюється крапля. Поверхня краплі розтягується під дією сили тяжіння, що діє на рідину. (рис. 23.2). Сила тяжіння тягне краплю вниз, збільшуючи розмір кулі – краплі, а сила поверхневого натягу намагається скоротити поверхню «плівки». В момент відриву краплі вага краплі – Коефіцієнт поверхневого натягу для даної рідини можна визначити з рівняння
де
Виключивши з рівнянь (23.4) і (23.5)
Таким чином, визначивши об’єми
|

 Між молекулами рідини діють Ван-дер-Ваальсівські сили притягання, які швидко зменшуються із збільшенням відстані між молекулами (
Між молекулами рідини діють Ван-дер-Ваальсівські сили притягання, які швидко зменшуються із збільшенням відстані між молекулами (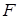 ~
~ 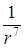 ).
).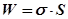 , (23.1)
, (23.1)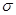 – коефіцієнт поверхневого натягу. З механіки відомо, що положення рівноваги тіла відповідає мінімуму потенціальної енергії, тому за умови відсутності зовнішніх сил рідина приймає форму з мінімальною поверхнею, тобто форму кулі. Наявність поверхневої енергії зумовлює намагання рідини скоротити свою поверхню. Поверхневий шар рідини поводить себе як пружна плівка, яка намагається скоротитись. У ній діють сили поверхневого натягу.
– коефіцієнт поверхневого натягу. З механіки відомо, що положення рівноваги тіла відповідає мінімуму потенціальної енергії, тому за умови відсутності зовнішніх сил рідина приймає форму з мінімальною поверхнею, тобто форму кулі. Наявність поверхневої енергії зумовлює намагання рідини скоротити свою поверхню. Поверхневий шар рідини поводить себе як пружна плівка, яка намагається скоротитись. У ній діють сили поверхневого натягу.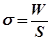 . (23.2)
. (23.2) або
або 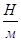 .
. , (23.3)
, (23.3)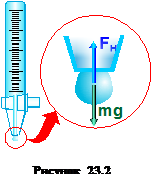
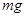 дорівнює силі поверхневого натягу, яка рівна
дорівнює силі поверхневого натягу, яка рівна  . Тоді
. Тоді 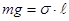 , де
, де  – довжина шийки, по якій відбувається розрив «плівки» поверхневого шару.
– довжина шийки, по якій відбувається розрив «плівки» поверхневого шару.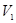 , густиною
, густиною  і відомим коефіцієнтом поверхневого натягу
і відомим коефіцієнтом поверхневого натягу 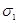 . Якщо ця рідина витікає краплями в кількості
. Якщо ця рідина витікає краплями в кількості 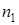 , то очевидно
, то очевидно , (23.4)
, (23.4) – вага рідини,
– вага рідини, 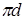 - довжина шийки
- довжина шийки  . Для рідини з невідомим коефіцієнтом поверхневого натягу
. Для рідини з невідомим коефіцієнтом поверхневого натягу  , об’ємом
, об’ємом 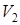 , густиною
, густиною 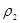 і кількістю утворених з цього об’єму крапель
і кількістю утворених з цього об’єму крапель 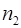 можна записати
можна записати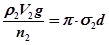 . (23.5)
. (23.5)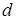 , отримуємо:
, отримуємо: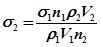 . (23.6)
. (23.6) рідин, кількість крапель
рідин, кількість крапель 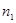 і
і 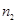 та табличне значення
та табличне значення 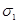 , можна визначити поверхневий натяг невідомої рідини. Якщо взяти об’єми однаковими, то в формулі (23.6) можна їх скоротити і вона набуде вигляду:
, можна визначити поверхневий натяг невідомої рідини. Якщо взяти об’єми однаковими, то в формулі (23.6) можна їх скоротити і вона набуде вигляду: . (23.7)
. (23.7)


