ВИЗНАЧЕННЯ КОЕФІЦІЄНТА ВНУТРІШНЬОГО ТЕРТЯ І СЕРЕДНЬОЇ ДОВЖИНИ ВІЛЬНОГО ПРОБІГУ МОЛЕКУЛ ПОВІТРЯ
Мета роботи: вивчити теорію явищ переносу в газах, визначити коефіцієнт внутрішнього тертя повітря і обчислити довжину вільного пробігу молекул повітря.
Обладнання: установка для визначення коефіцієнта внутрішнього тертя і середньої довжини вільного пробігу молекул повітря.
Теоретичні відомості
Середня довжина вільного пробігу молекул  - середня відстань, яку молекула проходить від одного зіткнення до другого.
- середня відстань, яку молекула проходить від одного зіткнення до другого.
Ефективний діаметр молекули 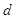 визначає мінімальну відстань, на яку можуть зблизитись центри двох молекул. Довжина вільного пробігу молекул залежить від ефективного діаметра молекул та концентрації:
визначає мінімальну відстань, на яку можуть зблизитись центри двох молекул. Довжина вільного пробігу молекул залежить від ефективного діаметра молекул та концентрації:
 , (22.1)
, (22.1)
де 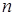 - концентрація молекул,
- концентрація молекул,  - ефективний діаметр молекул.
- ефективний діаметр молекул.
До явищ переносу в газах належать: дифузія (пов’язана з переносом маси); внутрішнє тертя (пов’язане з переносом імпульсу); теплопровідність (пов’язана з переносом енергії молекул).
У даній лабораторній роботі вивчається явище внутрішнього тертя.
При русі шарів газу з різними швидкостями між ними виникають сили внутрішнього тертя. Сила внутрішнього тертя в газі, як і в рідинах, пропорційна площі дотику шарів  і градієнту швидкості
і градієнту швидкості 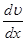 :
:
 , (22.2)
, (22.2)
де  - коефіцієнт внутрішнього тертя або коефіцієнт в’язкості.
- коефіцієнт внутрішнього тертя або коефіцієнт в’язкості.
 Градієнт швидкості
Градієнт швидкості 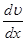 характеризує зміну швидкості з відстанню при переході від одного шару до другого в напрямі, перпендикулярному до напряму руху шарів (рис. 22.1).
характеризує зміну швидкості з відстанню при переході від одного шару до другого в напрямі, перпендикулярному до напряму руху шарів (рис. 22.1).
Коефіцієнт в’язкості чисельно дорівнює силі внутрішнього тертя, що діє на одиницю площі дотику шарів при градієнті швидкості рівному одиниці.
Фізичний зміст коефіцієнта в’язкості в газах полягає в тому, що він кількісно дорівнює імпульсу, який переноситься за одиницю часу через одиницю площі при градієнті швидкості, рівному одиниці.
Молекулярно-кінетична теорія газів дає вираз для коефіцієнта в’язкості
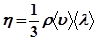 , (22.3)
, (22.3)
де 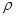 - густина газу;
- густина газу;  - середня арифметична швидкість молекул газу;
- середня арифметична швидкість молекул газу;  - середня довжина вільного пробігу молекул. З рівняння (22.3) випливає, що в’язкість газів не залежить від тиску. Дійсно, з основного рівняння молекулярно кінетичної теорії маємо, що
- середня довжина вільного пробігу молекул. З рівняння (22.3) випливає, що в’язкість газів не залежить від тиску. Дійсно, з основного рівняння молекулярно кінетичної теорії маємо, що  , тобто тиск прямо пропорційний концентрації молекул, а густина
, тобто тиск прямо пропорційний концентрації молекул, а густина 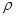 - також пропорційна концентрації, а значить і тиску.
- також пропорційна концентрації, а значить і тиску.
Отже при сталій температурі  ~
~ 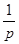 (див. формулу (22.1)), а густина
(див. формулу (22.1)), а густина 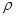 ~
~ 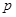 . Середня арифметична швидкість від тиску не залежить, тому згідно (22.3) в’язкість газів не залежить від тиску. З іншого боку концентрація молекул від температури не залежить, а середня арифметична швидкість пропорційна
. Середня арифметична швидкість від тиску не залежить, тому згідно (22.3) в’язкість газів не залежить від тиску. З іншого боку концентрація молекул від температури не залежить, а середня арифметична швидкість пропорційна 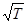 . Тому в’язкість газів зростає з підвищенням температури. З формули (22.3) можна визначити середню довжину вільного пробігу молекул, якщо відомо
. Тому в’язкість газів зростає з підвищенням температури. З формули (22.3) можна визначити середню довжину вільного пробігу молекул, якщо відомо  ,
, 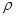 і
і  . В’язкість
. В’язкість  знаходять, користуючись формулою Пуазейля:
знаходять, користуючись формулою Пуазейля:
 , (22.4)
, (22.4)
де 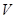 - об’єм рідини, що проходить крізь капіляр;
- об’єм рідини, що проходить крізь капіляр; 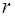 - радіус капіляра;
- радіус капіляра; 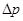 - різниця тисків на кінцях капіляра;
- різниця тисків на кінцях капіляра;  - довжина капіляра.
- довжина капіляра.
Якщо різницю тисків вимірювати за допомогою водяного манометра, то  , де
, де 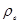 - густина води;
- густина води;  - прискорення земного тяжіння;
- прискорення земного тяжіння; 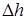 - різниця висот в колінах манометра. Тепер формула (22.4) набуває вигляду:
- різниця висот в колінах манометра. Тепер формула (22.4) набуває вигляду:
 . (22.5)
. (22.5)
Густину повітря знайдемо з рівняння Клапейрона-Менделеєва
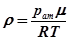 , (22.6)
, (22.6)
де 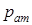 - атмосферний тиск;
- атмосферний тиск; 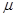 - молярна маса повітря, яка дорівнює
- молярна маса повітря, яка дорівнює  ;
;  - універсальна газова стала;
- універсальна газова стала;  - абсолютна температура повітря. Тиск вимірюється за допомогою барометра в мм. рт. ст.. В паскалях це буде:
- абсолютна температура повітря. Тиск вимірюється за допомогою барометра в мм. рт. ст.. В паскалях це буде:
 , (22.7)
, (22.7)
де 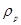 - густина ртуті, рівна
- густина ртуті, рівна  ;
;  - атмосферний тиск, виражений в метрах ртутного стовпа.
- атмосферний тиск, виражений в метрах ртутного стовпа.
Підставши рівняння (22.7) в (22.6), отримаємо:
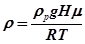 . (22.8)
. (22.8)
Середня арифметична швидкість, як відомо, дорівнює:
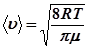 . (22.9)
. (22.9)
Підставимо в формулу (22.3) вирази (22..8) і (22.9) і знайдемо  :
:
 . (22.10)
. (22.10)

 - середня відстань, яку молекула проходить від одного зіткнення до другого.
- середня відстань, яку молекула проходить від одного зіткнення до другого.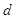 визначає мінімальну відстань, на яку можуть зблизитись центри двох молекул. Довжина вільного пробігу молекул залежить від ефективного діаметра молекул та концентрації:
визначає мінімальну відстань, на яку можуть зблизитись центри двох молекул. Довжина вільного пробігу молекул залежить від ефективного діаметра молекул та концентрації: , (22.1)
, (22.1)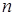 - концентрація молекул,
- концентрація молекул,  - ефективний діаметр молекул.
- ефективний діаметр молекул. і градієнту швидкості
і градієнту швидкості 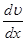 :
: , (22.2)
, (22.2) - коефіцієнт внутрішнього тертя або коефіцієнт в’язкості.
- коефіцієнт внутрішнього тертя або коефіцієнт в’язкості. Градієнт швидкості
Градієнт швидкості 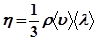 , (22.3)
, (22.3)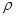 - густина газу;
- густина газу;  - середня арифметична швидкість молекул газу;
- середня арифметична швидкість молекул газу;  , тобто тиск прямо пропорційний концентрації молекул, а густина
, тобто тиск прямо пропорційний концентрації молекул, а густина 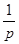 (див. формулу (22.1)), а густина
(див. формулу (22.1)), а густина 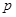 . Середня арифметична швидкість від тиску не залежить, тому згідно (22.3) в’язкість газів не залежить від тиску. З іншого боку концентрація молекул від температури не залежить, а середня арифметична швидкість пропорційна
. Середня арифметична швидкість від тиску не залежить, тому згідно (22.3) в’язкість газів не залежить від тиску. З іншого боку концентрація молекул від температури не залежить, а середня арифметична швидкість пропорційна 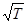 . Тому в’язкість газів зростає з підвищенням температури. З формули (22.3) можна визначити середню довжину вільного пробігу молекул, якщо відомо
. Тому в’язкість газів зростає з підвищенням температури. З формули (22.3) можна визначити середню довжину вільного пробігу молекул, якщо відомо  , (22.4)
, (22.4)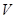 - об’єм рідини, що проходить крізь капіляр;
- об’єм рідини, що проходить крізь капіляр; 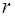 - радіус капіляра;
- радіус капіляра; 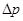 - різниця тисків на кінцях капіляра;
- різниця тисків на кінцях капіляра;  - довжина капіляра.
- довжина капіляра. , де
, де 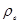 - густина води;
- густина води;  - прискорення земного тяжіння;
- прискорення земного тяжіння; 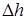 - різниця висот в колінах манометра. Тепер формула (22.4) набуває вигляду:
- різниця висот в колінах манометра. Тепер формула (22.4) набуває вигляду: . (22.5)
. (22.5)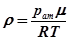 , (22.6)
, (22.6)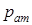 - атмосферний тиск;
- атмосферний тиск; 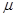 - молярна маса повітря, яка дорівнює
- молярна маса повітря, яка дорівнює  ;
;  - універсальна газова стала;
- універсальна газова стала;  - абсолютна температура повітря. Тиск вимірюється за допомогою барометра в мм. рт. ст.. В паскалях це буде:
- абсолютна температура повітря. Тиск вимірюється за допомогою барометра в мм. рт. ст.. В паскалях це буде: , (22.7)
, (22.7)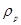 - густина ртуті, рівна
- густина ртуті, рівна  ;
;  - атмосферний тиск, виражений в метрах ртутного стовпа.
- атмосферний тиск, виражений в метрах ртутного стовпа.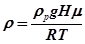 . (22.8)
. (22.8)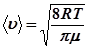 . (22.9)
. (22.9) . (22.10)
. (22.10)


