Лабораторна робота № 20
ВИЗНАЧЕННЯ КОЕФІЦІЄНТА ВНУТРІШНЬОГО ТЕРТЯ В РІДИНАХ МЕТОДОМ СТОКСА Мета роботи: визначити коефіцієнт внутрішнього тертя касторового або іншого масла. Порівняти одержане значення з табличним і зробити відповідні висновки. Обладнання: скляний циліндр з маслом, мікрометр, секундомір, кульки, масштабна лінійка.
Теоретичні відомості Внутрішнє тертя (одне з явищ переносу) полягає у виникненні сил взаємодії між шарами рідини чи газу, що рухаються паралельно один одному з різними, за модулем, швидкостями. Зі сторони шару, що рухається скоріше, на шар, що рухається повільніше, діє прискорююча сила, і навпаки, шар, що рухається з меншою швидкістю, гальмує шар, що рухається з більшою швидкістю. Сили тертя, що виникають при цьому, напрямлені по дотичній до поверхні дотику шарів. Згідно із законом Ньютона сила внутрішнього тертя
де
Коефіцієнт внутрішнього тертя, як видно з формули (20.1), чисельно рівний силі внутрішнього тертя, що діє на одиницю площі дотику шарів при одиничному градієнті швидкості. Вимірюється коефіцієнт динамічної в’язкості рідин у Па·с. Одним з експериментальних методів визначення коефіцієнта динамічної в’язкості є метод Стокса (метод падаючої кульки). Якщо кулька, що змочується рідиною, падає в рідині і не залишає за собою ніяких завихрень (стала швидкість падіння, незначний радіус кульки), то, як показав Стокс, сила опору рівна:
де Між шаром рідини, що прилип до кульки, і сусіднім шаром виникає сила тертя, яка заставляє його зміщуватись в напрямку руху. Швидкість наступних шарів буде тим меншою, чим дальше вони знаходяться від кульки. Якщо радіус
Рівняння (20.3) в проекціях на вертикальний напрям запишеться так:
Враховуючи, що
Тоді
де
Так як
|

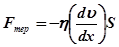 , (20.1)
, (20.1)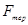 - сила тертя;
- сила тертя;  -коефіцієнт внутрішнього тертя (динамічної в’язкості);
-коефіцієнт внутрішнього тертя (динамічної в’язкості); - градієнт швидкості;
- градієнт швидкості;  - площа дотику шарів.
- площа дотику шарів.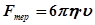 , (20.2)
, (20.2) - швидкість кульки;
- швидкість кульки; 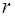 - радіус кульки.
- радіус кульки.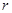 кульки набагато менший за радіус посудини R, то поблизу стінок посудини швидкість руху шарів буде рівна нулю.
кульки набагато менший за радіус посудини R, то поблизу стінок посудини швидкість руху шарів буде рівна нулю. На кульку, що падає в рідині (рис. 20.1), діють три сили:
На кульку, що падає в рідині (рис. 20.1), діють три сили: 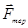 - сила тертя;
- сила тертя; 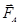 - виштовхувальна сила Архімеда,
- виштовхувальна сила Архімеда,  - сила тяжіння. Якщо кулька рухається рівномірно то
- сила тяжіння. Якщо кулька рухається рівномірно то . (20.3)
. (20.3)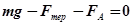 . (20.4)
. (20.4) ,
, 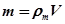 , а об’єм кульки
, а об’єм кульки 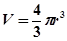 рівняння (20.4) набере вигляду:
рівняння (20.4) набере вигляду: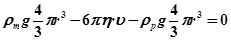 .
. , (20.5)
, (20.5) - густина речовини кульки,
- густина речовини кульки, 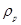 - густина рідини,
- густина рідини,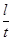 , r – радіус кульки.
, r – радіус кульки.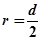 , том робоча формула матиме вигляд:
, том робоча формула матиме вигляд: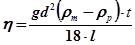 . (20.6)
. (20.6)


