Лабораторна робота № 24
ВИЗНАЧЕННЯ ВІДНОШЕННЯ Мета роботи:вивчення адіабатного процесу і визначення показника адіабати повітря. Обладнання: прилад Клемана–Дезорма. Теоретичні відомості Адіабатним процесом називається процес, який відбувається без теплообміну з навколишнім середовищем. Оскільки для адіабатного процесу Q = 0, то перший закон термодинаміки (Q = ΔU + A) запишеться так: ΔU = – A або A = U1 – U2, тобто робота при адіабатному розширенні газу виконується за рахунок зменшення його внутрішньої енергії, а виконана робота при адіабатному стисненні газу іде на збільшення його внутрішньої енергії. Адіабатний процес описується рівнянням Пуассона:
де Якщо відомі температури і тиски, то рівняння адіабати можна записати так:
Теплоємність тіла - фізична величина, чисельно рівна кількості теплоти яку необхідно надати, щоб нагріти тіло на один градус Кельвіна:
Для однорідних речовин розрізняють теплоємність молярну та питому. Молярна теплоємність – фізична величина, чисельно рівна кількості теплоти, необхідної для нагрівання одного моля речовини на один градус Кельвіна:
Питома теплоємність – фізична величина, чисельно рівна кількості теплоти, необхідної для нагрівання одиниці маси речовини на один градус Кельвіна:
Питома теплоємність позначається малою літерою с, а молярна − великою (СV, Cp). Між ними існує зв’язок – Для газів різнять дві теплоємності: за сталого об’єму і за сталого тиску. Якщо нагрівання газу відбувається за сталого об’єму, то вся підведена до тіла теплота іде на збільшення внутрішньої енергії. Якщо ж ту саму кількість газу нагрівають в тому ж інтервалі температур при сталому тиску, то газ розширюється, а це значить, що крім теплоти, яка йде на збільшення внутрішньої енергії, потрібна ще додаткова кількість теплоти для виконання роботи розширення газу. Тому Сp>CV. Зв’язок між Сp і CV описується рівнянням Мейєра
де R – універсальна газова стала, чисельно рівна роботі ізобарного розширення одного моля газу при його нагріванні на 1К. Як відомо з молекулярно – кінетичної теорії газів
де i – число ступенів вільності. Для одноатомних газів i = 3, для двоатомних i = 5 і для багатоатомних i = 6. Одним із методів визначення При закритому крані К2 в балон нагнітають деяку кількість повітря і закривають кран К1. Черездеякий час внаслідок теплообміну із зовнішнім середовищем температура повітря в балоні, яка зросла при накачуванні, знизиться до температури навколишнього середовища, а тиск стане вище атмосферного на величину Таким, чином повітря в балоні буде характеризуватись параметрами Таким чином, в кінці адіабатного процесу повітря буде характеризуватись тиском
Відношення температур можна виразити через відношення тисків, виходячи із таких міркувань: нова маса повітря в балоні після закриття крану К2 має температуру
або
З рівнянь (24.4) і (24.6) отримаємо:
Прологарифмувавши рівняння (24.4) і, розв’язавши його відносно
Розкладемо Підставивши одержані вирази у формулу (24.8), одержимо робочу формулу:
|

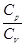 ДЛЯ ПОВІТРЯ МЕТОДОМ КЛЕМАНА–ДЕЗОРМА
ДЛЯ ПОВІТРЯ МЕТОДОМ КЛЕМАНА–ДЕЗОРМА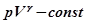 , (24.1)
, (24.1) - тиск;
- тиск;  об’єм;
об’єм; 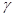 - показник адіабати. Показник адіабати визначається відношенням
- показник адіабати. Показник адіабати визначається відношенням 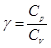 , де
, де  – молярна теплоємність газі при сталому тиску, а
– молярна теплоємність газі при сталому тиску, а 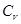 – молярна теплоємність газу при сталому об’ємі.
– молярна теплоємність газу при сталому об’ємі. . (24.2)
. (24.2)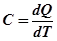 .
.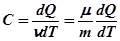 .
. .
. , де
, де  – молярна маса речовини.
– молярна маса речовини.
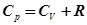 , (24.3)
, (24.3) , а
, а 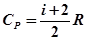 ,
,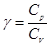 є метод Клемана − Дезорма. Він полягає в наступному: кран К1 з’єднує балон з насосом, а К2 − з навколишнім середовищем (рис. 24.1).
є метод Клемана − Дезорма. Він полягає в наступному: кран К1 з’єднує балон з насосом, а К2 − з навколишнім середовищем (рис. 24.1). , де
, де  − різниця висот рідини в колінах манометра,
− різниця висот рідини в колінах манометра,  − густина води.
− густина води. V1, T 1, де
V1, T 1, де  − об’єм балона,
− об’єм балона,  − температура в балоні, яка дорівнює температурі навколишнього середовища. Відкриваємо кран К2. Повітря почне швидко розширюватися. Внаслідок того, що розширення відбувається дуже швидко, процес можна вважати адіабатним. Тиск в балоні почне падати. Коли він стане рівним атмосферному, на що вкаже рівність рівнів рідини в колінах манометра, закриємо кран К2.
− температура в балоні, яка дорівнює температурі навколишнього середовища. Відкриваємо кран К2. Повітря почне швидко розширюватися. Внаслідок того, що розширення відбувається дуже швидко, процес можна вважати адіабатним. Тиск в балоні почне падати. Коли він стане рівним атмосферному, на що вкаже рівність рівнів рідини в колінах манометра, закриємо кран К2.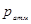 і температурою
і температурою  . Зв’язок між параметрами повітря на початку адіабатного процесу і в його кінці можна записати, використавши рівняння (24.2):
. Зв’язок між параметрами повітря на початку адіабатного процесу і в його кінці можна записати, використавши рівняння (24.2):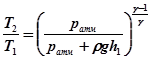 . (24.4)
. (24.4) , де
, де 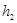 − різниця висот рідини в колінах манометра. Тобто відбувається ізохорний процес, для якого
− різниця висот рідини в колінах манометра. Тобто відбувається ізохорний процес, для якого (24.5)
(24.5) . (24.6)
. (24.6) . (24.7)
. (24.7)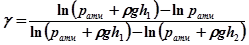 (24.8)
(24.8) і
і  в ряд Маклорена і обмежимось першими двома членами:
в ряд Маклорена і обмежимось першими двома членами:  ;
;  .
. . (24.9)
. (24.9)


