Лабораторна робота № 26
ВИЗНАЧЕННЯ КОЕФІЦІЄНТА В'ЯЗКОСТІ ПОВІТРЯ КАПІЛЯРНИМ МЕТОДОМ
Мета роботи:вивчення внутрішнього тертя повітря як одного з явищ переносу в газах. Обладнання:експериментальна установка ФПТ 1-1. Теоретичні відомості Явища переносу - це процеси встановлення рівноваги в системі шляхом переносу маси (дифузія), енергії (теплопровідність) та імпульсу молекул (внутрішнє тертя, або в'язкість). Усі ці явища обумовлені тепловим рухом молекул. При явищі в'язкості спостерігається перенос імпульсу від молекул із шарів потоку, які рухаються швидше, до повільніших. Наприклад, у випадку протікання рідини або газу прямолінійною циліндричною трубою (капіляром) за малих швидкостей потоку течія є ламінарною, тобто потік газу рухається окремими шарами, які не перемішуються між собою. У цьому випадку шари являють собою сукупність нескінченно тонких циліндричних поверхонь, вкладених одна в одну, які мають спільну вісь, що збігається з віссю труби. Внаслідок хаотичного теплового руху молекули безперервно переходять із шару в шар і при зіткненнях з іншими молекулами обмінюються імпульсами спрямованого руху. При переході із шару з більшою швидкістю спрямованого руху в шар із меншою швидкістю молекули переносять у другий шар свій імпульс спрямованого руху. У "більш швидкий" шар переходять молекули з меншим імпульсом. У результаті перший шар гальмується, а другий - прискорюється. Дослід показує, що імпульс dP, що передається від шару до шару через поверхню площею S, пропорційний градієнту швидкості
У результаті між шарами виникає сила внутрішнього тертя
де η - коефіцієнт в'язкості. Для ідеального газу
де ρ - густина газу; < λ>; - середня довжина вільного пробігу молекул; <υ;Т > -середня швидкість теплового руху молекул, Виділимо в капілярі уявний циліндричний об'єм газу радіуса r і довжини l, як показано на рисунку 26.1.
Рисунок 26.1 – До розрахунку об’ємної витрати газу в разі протікання його через капіляр
Позначимо тиски на його торцях Р 1і Р 2. При установленій течії сила тиску на циліндр F = (Р 1 -Р 2 )·π·r2 врівноважується силою внутрішнього тертя F Tщо діє на бічну поверхню циліндра з боку зовнішніх шарів газу:
F - F T = 0. (26.2)
Сила внутрішнього тертя визначається за формулою Ньютона (26.1). Зважаючи на те, що S=2·π·r·l і швидкість υ;(r) зменшується при віддаленні від осі труби, тобто
У цьому випадку умова стаціонарності (26.2) запишеться у вигляді:
Інтегруючи цю рівність, одержимо
де С – стала інтегрування, яка визначається з граничних умов. Для r = R швидкість газу повинна дорівнювати нулю, оскільки сила внутрішнього тертя об стінку капіляра гальмує суміжний з нею шар газу. Тоді
Підставивши (26.6) у (26.5), одержимо
Обчислимо об’ємну витрату газу Q, тобто об’єм, що протікає за одиницю часу через поперечний переріз труби. Через кільцеву площадку з внутрішнім радіусом r і зовнішнім r + dr щосекунди протікає об’єм газу dQ=2·π·r·dr·υ(r). Тоді
або
Формулу (26.8), яку називають формулою Пуазейля, можна використовувати для експериментального визначення коефіцієнта в'язкості газу. Формулу Пуазейля було одержано в припущенні ламінарної течії газу або рідини. Однак із збільшенням швидкості потоку рух стає турбулентним і шари перемішуються. За турбулентного руху швидкість у кожній точці змінює своє значення та напрям і зберігається тільки середнє значення швидкості. Характер руху рідини або газу в трубі визначається числом Рейнольдса:
де < υ> - середня швидкість потоку; ρ - густина рідини або газу, R – радіус труби. У гладких циліндричних каналах перехід від ламінарної течії до турбулентної відбувається при Re ≈ 1000. Тому в разі використання формули Пуазейля необхідно забезпечити виконання умови Re<;1000. Крім того, експеримент необхідно ставити таким чином, щоб стисливістю газу можна знехтувати. Це можливо тоді, коли перепад тисків вздовж капіляра значно менший від самого тиску. У даній установці тиск газу дещо більший від атмосферного (103 см. вод. ст.), а перепад тисків становить від ~ 10 см. вод. ст., тобто приблизно 1 % від атмосферного. Формула (26.8) справедлива для ділянки труби, в якій встановилась стала течія з квадратичним законом розподілу швидкостей (26.7) по перерізу труби. Така течія встановлюється на деякій відстані від входу в капіляр, тому для досягнення достатньої точності експерименту необхідне виконання умови R<<l, де R - радіус; l - довжина капіляра.
|

 , площі S та часу переносу dt:
, площі S та часу переносу dt: .
. , (26.1)
, (26.1)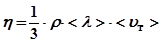 ,
,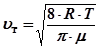 ; μ – молекулярна маса газу; R – універсальна газова стала.
; μ – молекулярна маса газу; R – універсальна газова стала.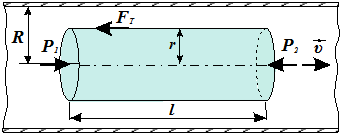
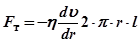 . (26.3)
. (26.3) . (26.4)
. (26.4) , (26.5)
, (26.5) . (26.6)
. (26.6) . (26.7)
. (26.7)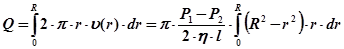
 . (26.8)
. (26.8) , (26.9)
, (26.9)


