Лабораторна робота № 27
ВИЗНАЧЕННЯ КОЕФІЦІЄНТА ТЕПЛОПРОВІДНОСТІ МЕТОДОМ НАГРІТОЇ НИТКИ
Мета роботи: вивчення теплопровідності повітря, як одного з явищ переносу в газах. Обладнання: експериментальна установка ФПТ 1-3 Теоретичні відомості Поширення теплоти у газах відбувається трьома способами: тепловим випромінюванням (перенос енергії електромагнітними хвилями), конвекцією (перенос енергії за рахунок переміщення шарів газу в просторі з областей з більш високою температурою в області з нижчою температурою) та теплопровідністю. Теплопровідність - це процес передачі теплоти від більш нагрітого шару газу до менш нагрітого за рахунок хаотичного теплового руху молекул. При теплопровідності відбувається безпосередня передача енергії від молекул, що мають більшу енергією, до тих, що мають меншу. Для стаціонарного процесу, за якого різниця температур у шарі газу не змінюється з часом, кількість теплоти δQ, яка переноситься внаслідок теплопровідності за час dτ через поверхню площею S, перпендикулярну до напряму переносу енергії, в напрямі зменшення температури, визначається законом Фур'є:
де χ; - коефіцієнт теплопровідності; dТ/dr - градієнт температури. Для ідеального газу
де ρ -густина газу; < λ> - середня довжина вільного пробігу молекули; <υ;T > - середня швидкість теплового руху молекул, Розглянемо два коаксіальних циліндри, простір між якими заповнено газом. Якщо внутрішній циліндр нагрівати, а температуру зовнішнього циліндра підтримувати сталою, нижчою за температуру нагрівача, то в кільцевому шарі газу виникає радіальний потік теплоти, направлений від внутрішнього циліндра до зовнішнього. При цьому температури шарів газу, прилеглих до стінок циліндрів, дорівнюють температурі стінок. Виділимо у газі кільцевий шар радіусом r, товщиною dr і довжиною L. За законом Фур'є (27.1) тепловий потік q=δQ/dτ;, тобто кількість теплоти, що проходить через цей шар за одну секунду, можна записати у вигляді
Розділивши змінні, одержимо
Тоді
або
В (27.4) Т 1, R 1і Т2, R2 - відповідно температури поверхонь та радіуси внутрішнього і зовнішнього циліндрів. З рівняння (27.4) одержуємо формулу для визначення коефіцієнта теплопровідності газу:
Формулу (27.5) одержано у припущенні, що теплота переноситься від внутрішнього до зовнішнього циліндра тільки завдяки теплопровідності. Це припущення є достатньо обґрунтованим, оскільки потік променистої енергії при невисоких температурах і малому діаметрі нагрівника становить незначну частину кількості теплоти, що переноситься, а конвекція усувається підбором діаметра зовнішнього циліндра та його вертикальним розміщенням в експериментальній установці. Внутрішнім циліндром може служити тонка дротина (нитка), звичайно вольфрамова, яка нагрівається електричним струмом. Тоді після встановлення стаціонарного режиму тепловий потік можна прийняти таким, що дорівнює потужності електричного струму у дротині
де J H - струм через дротину; Uн - спад напруги на дротині. Якщо послідовно з дротиною підключити еталонний резистор опору RР, то
і тоді
де Uр - спад напруги на еталонному резисторі. Використовуючи рівність (27.6) у формулі (27.5), одержимо
де D і d - діаметри зовнішнього циліндра й дротини; ΔТ =ТН - ТТ -різниця температур дротини і зовнішнього циліндра (трубки). Температуру трубки ТT можна взяти такою, що дорівнює температурі навколишнього повітря. Для обчислення різниці температур ΔТ у шарі газу запишемо формули, що визначають опір дротини при температурі навколишнього повітря і у нагрітому стані:
де R 0 - опір дротини при t=0 °С; α; - температурний коефіцієнт опору матеріалу дротини. Виключивши з цих рівнянь R0, знайдемо
Враховуючи, що
де UH, UH 0 - спад напруги на дротині відповідно у нагрітому стані і при температурі навколишнього повітря t0; UР, Uр0 - спад напруги на еталонному резисторі відповідно при нагрітій дротині і при температурі навколишнього повітря t0.
|

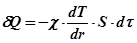 , (27.1)
, (27.1) , (27.2)
, (27.2)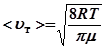 ; С V - питома теплоємність газу за сталого об'єму.
; С V - питома теплоємність газу за сталого об'єму. . (27.3)
. (27.3) .
.
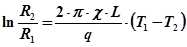 . (27.4)
. (27.4) . (27.5)
. (27.5)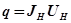 ,
,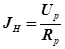 ,
,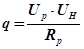 , (27.6)
, (27.6)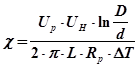 ,(27.7)
,(27.7)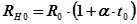 ,
,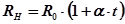 ,
, .
. ,
,  ,
, 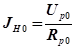 , отримаємо
, отримаємо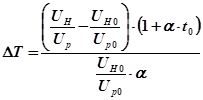 , (27.8)
, (27.8)


