Лабораторна робота № 28
ВИЗНАЧЕННЯ ВІДНОШЕННЯ ТЕПЛОЄМНОСТЕЙ ПОВІТРЯ ЗА СТАЛИХ ТИСКУ Й ОБ'ЄМУ РЕЗОНАНСНИМ МЕТОДОМ
Мета роботи:вивчення процесу поширення звукової хвилі, вимірювання швидкості звуку у повітрі за різних температур та визначення відношеннятеплоємностей Обладнання:експериментальна установка ФПТ 1-7. Теоретичні відомості Пружними хвилями називають механічні збурення, які поширюються у пружному середовищі. Нехай вздовж однорідного циліндричного зразка з площею поперечного перерізу S поширюється пружна поздовжня хвиля. Отже, разом із швидкістю υ поширюється відносна деформація
де l - довжина виділеної частини зразка.
Рисунок 28.1 - Схема поширення збурення вздовж однорідного зразка Стисканню відповідає збільшення густини, отже, густина в області стискання
Тут ми врахували, що площа поперечного перерізу S зразка не змінюється при поширенні поздовжньої хвилі. У формулі (28.2) помножимо чисельник і знаменник на величину (l + Δl):
Враховуючи, що Δl 2 <<l 2, отримаємо:
Звідси, враховуючи формулу (28.1), маємо
або Δρ = ρε;. (28.3)
Поширення збурення являє собою рух області стискання із швидкістю υ вздовж зразка. За проміжок часу dt через поперечний переріз пройде ділянка стискання довжиною dx = υdt. Маса цієї ділянки dm=Δρ·S·dx або, враховуючи (28.3), dm=ρ·ε·S·υ·dt. Маса dm рухається зі швидкістю υ; і має імпульс υ·dm = ρ·ε·S·υ;2 ·dt. Записуючи силу пружності за законом Гука, отримаємо
де Е – модуль пружності, звідки
F = E · ε · S.
З міна імпульсу маси dm (оскільки до проходження збурювання ця маса перебувала у спокої) за другим законом Ньютона дорівнює добуткові діючої на неї сили пружності і часу її дії. Отже F·dt = ρ· ε · S · υ2 · dt або E · ε · S · dt= ρ· ε · S · υ2 · dt,
звідки
і швидкість поширення поздовжньої пружної хвилі
Якщо пружна хвиля поширюється у газі, який міститься у гладенькій прямолінійній трубі зі сталим поперечним перерізом, то враховуючи, що на відміну від твердих тіл гази не чинять опору зсуву, в них можуть виникати тільки поздовжні хвилі, і, отже, швидкість поширення пружної хвилі в газі може обчислюватись за формулою (28.5). Визначимо величину Е для газу. Якщо за дії сили F на деякий об'єм газу тиск у ньому одержить приріст ΔР по відношенню до тиску газу Р в незбуреному стані, то за аналогією з (28.4)
Вважаючи зміни тиску dP і об'єму dV нескінченно малими, можна записати, що
де знак мінус означає, що збільшення тиску відповідає зменшенню об'єму. Нехай у газі поширюється звукова хвиля, яка являє собою пружну хвилю малої інтенсивності, здатну викликати відчуття звуку, з частотою від 16 до 20000 Гц. Коливання густини у звуковій хвилі відбуваються так швидко, що теплообмін між шарами газу, які мають різні температури, не встигає відбутися. Тому процес поширення звукової хвилі в газі можна вважати адіабатичним і до нього можна застосувати рівняння Пуассона (28.11). Диференціюючи це рівняння, отримаємо
V γ · dP + γ · P · V γ-1 · dV = 0, звідки
З (28.6) і (28.7) знайдемо
E = γ · P. (28.8)
Визначивши Р з рівняння Клапейрона-Менделєєва і враховуючи, що густина газу
Підставимо значення Р у (28.8), тоді
Підставивши співвідношення (28.9) у формулу (28.5), матимемо формулу Лапласа для розрахунку швидкості звуку в газі:
з якої
Таким чином, для визначення відношення теплоємностей газу γ достатньо виміряти його температуру Т та швидкість поширення звуку υ; у цьому газі. Швидкість звуку за даної температури може бути визначена резонансним методом. Під час поширення хвилі вздовж закритого каналу, вона багаторазово відбивається від торців, і звукові коливання в каналі є результатом накладання цих відбитих хвиль. Якщо довжина каналу L дорівнює цілому числу півхвиль
2 · L · v 0 = n · υ, (28.12)
де v 0 - резонансна частота. Залежність (28.12) резонансної частоти від числа п може бути перевірена експериментально. Змінюючи частоту коливань за сталої довжини каналу, необхідно побудувати графік залежності v 0 = f(п), за кутовим коефіцієнтом якого
|

 .
. (рис. 28.1). Виділивши деяку частину зразка, знайдемо густину недеформованого середовища:
(рис. 28.1). Виділивши деяку частину зразка, знайдемо густину недеформованого середовища: , (28.1)
, (28.1)
 . (28.2)
. (28.2) .
. .
.
 , (28.4)
, (28.4)
 . (28.5)
. (28.5) .
. , (28.6)
, (28.6) . (28.7)
. (28.7)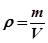 , отримаємо
, отримаємо .
.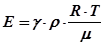 . (28.9)
. (28.9) , (28.10)
, (28.10)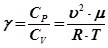 . (28.11)
. (28.11) (n - будь-яке ціле число, λ - довжина хвилі), то хвиля, відбита від торця каналу, повернувшись до його початку і знову відбиваючись, збігається по фазі з прямою хвилею. Такі хвилі підсилюють одна одну, амплітуда коливань при цьому різко зростає - настає резонанс. Під час звукових коливань шари газу, прилеглі до торців каналу, не зазнають зміщення. У цих місцях утворяться вузли зміщення, які повторюються через λ/2 по всій довжині каналу. Між вузлами знаходяться максимуми зміщення (пучності). Швидкість звуку υ; зв'язана з частотою коливань v і довжиною хвилі λ співвідношенням υ=λv, з урахуванням якого умову резонансу можна записати у вигляді
(n - будь-яке ціле число, λ - довжина хвилі), то хвиля, відбита від торця каналу, повернувшись до його початку і знову відбиваючись, збігається по фазі з прямою хвилею. Такі хвилі підсилюють одна одну, амплітуда коливань при цьому різко зростає - настає резонанс. Під час звукових коливань шари газу, прилеглі до торців каналу, не зазнають зміщення. У цих місцях утворяться вузли зміщення, які повторюються через λ/2 по всій довжині каналу. Між вузлами знаходяться максимуми зміщення (пучності). Швидкість звуку υ; зв'язана з частотою коливань v і довжиною хвилі λ співвідношенням υ=λv, з урахуванням якого умову резонансу можна записати у вигляді визначається швидкість звуку.
визначається швидкість звуку.


