Правила заокруглення у випадку математичних
операцій над числами
Обчислення певних фізичних величин, особливо якщо їх виконують за допомогою калькуляторів, потребують заокруглення сумарного числа. Необхідна точність розрахунків визначена тим, що розрахунок не повинен вносити у вимірювання додаткової похибки. Заокруглення в разі додавання і віднімання всіх чисел виконують до розряду на одиницю меншого, ніж розряд найменш точного числа. В результаті потрібно зберігати стільки десяткових знаків, скільки їх у наближеному заданому числі з найменшою кількістю десяткових знаків:
23,2 + 0,442 + 7,247 ≈ 23,2 + 0,44 + 7,25 = 30,89 ≈ 30,9 У результаті множення і ділення потрібно зберігати стільки значущих цифр, скільки їх має наближене задане число з найменшою кількістю значущих цифр:
30,9 · 1,8364 ≈ 30,9 · 1,84 = 56,856 ≈ 56,9. У разі піднесення до степеня в кінцевому результаті потрібно зберігати стільки значущих цифр, скільки їх має число, яке підносять до степеня:
(11,38)2 = 129,5044 ≈ 129,50 = 129,5.
У випадку знаходження коренів у результаті потрібно зберегти стільки значущих цифр, скільки їх має число, яке стоїть під коренем:
Під час обчислення проміжних результатів потрібно брати на одну цифру більше, ніж задано в заокругленнях у разі виконання математичних дій над числами. В кінцевому підсумку цю “запасну” цифру відкидають:
Запис результатів
Результат вимірювань записують у вигляді
f = f ср ± Δ f, ε(f) =... Наприклад, запис m = (1, 23 ± 0, 02) кг означає, що в результаті вимірювань для маси тіла знайдено значення 1,23 кг з абсолютною похибкою 0,02 кг і відносною похибкою
У записі виміряного значення останньою повинна бути цифра того десяткового розряду, який використовують у разі зазначення похибки. Наприклад, один і той же результат залежно від похибки, може мати вигляд
І т.д.
Зображення експериментальних результатів на графіках
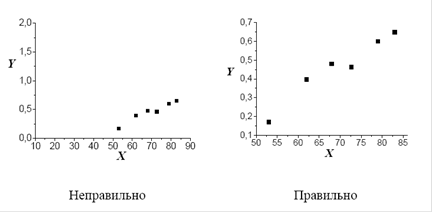
Результати експериментів відображають у вигляді не тільки таблиць, а й графіків. Для графіків ліпше використовувати спеціальний папір, наприклад, міліметровий або в клітинку. У разі побудови графіків потрібно розумно вибирати масштаб, щоб виміряні точки розташувались на всій площині аркуша. На рис. 1 зображені приклади правильної і неправильної побудови графіків. На лівому (неправильно побудованому) графіку експериментальні точки займають нижню праву частину рисунка. Щоб цього уникнути, потрібно вибрати більший масштаб по осі Y і змістити нуль абсцис, як це зроблено на правому графіку.
Рис. 1. Вибір масштабу та початку відліку в разі побудови графіків
Масштаб повинний бути зручним. Клітинка графіка чи міліметрового паперу може відповідати 0,1; 0,2; 0,5; 1,0; 2,0; 5,0; 10,0 одиницям величини, яку вимірюють, але не 2,5; 3,0; 4,0; 7,0 і т.д. Якщо масштаб незручний, то нанесення експериментальних точок на графік і використання графіка потребують багато часу, що часто призводить до помилок. Графічне зображення результатів дає змогу швидко зрозуміти характерні особливості залежності, яку спостерігають і виявити помилкові результати. Наприклад, з графіка на рис. 1 видно, що крива Y = Y (X) за збільшення Х стає пологішою. Третя ліворуч точка випала. Очевидно, під час її вимірювання була допущена помилка. Якщо це не так, то в інтервалі біля цієї точки шукана залежність має різко виражену особливість. Такі особливості становлять великий інтерес. Тому потрібно уважно виміряти область, розташовану поблизу точки, що випала, і намагатись детально вивчити форму кривої в інтервалі знайденої особливості. Точки, які наносяться на графіки, треба зображати чітко. Їх необхідно позначати олівцем, бо інакше помилково нанесену точку не можна буде видалити з графіка, не зіпсувавши його. Ніяких ліній і міток, які пояснюють побудову точок, на графік наносити не можна, оскільки вони заважають аналізувати результати.
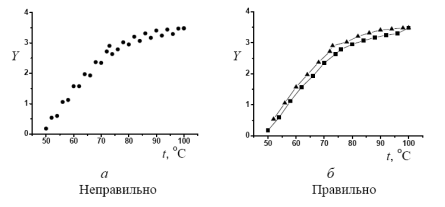
Рис. 2. Графічне зображення результатів, отриманих за різних умов
Точки, отримані за різних умов (під час нагрівання й охолодження, збільшення чи зменшення навантаження, у різні дні тощо, корисно наносити різними кольорами чи різними значками. Це допомагає побачити нові явища. Наприклад, на графіках рис. 2, а і б – один і той самий набір точок. На рис. 2, а всі ці точки нанесені однаково, а на рис. 2, б точки, отримані під час нагрівання й охолодження, зображені по-різному (трикутниками і квадратами). На першому з графіків видно тільки розкид точок, а другий свідчить, що розкид насправді невеликий, однак точки, виміряні під час нагрівання і під час охолодження, лежать на різних кривих. Очевидно, що тільки рис. 2, б містить необхідну інформацію для аналізу і побудований правильно. Спосіб зображення на графіку експериментальних результатів залежить від того, чи відома їхня випадкова похибка. Якщо вона не відома (що частіше всього буває), то результати зображають крапками, а якщо відома, то ліпше зображати їх не крапками, а хрестиками. Піврозмір хрестика по горизонталі повинен дорівнювати стандартній похибці по осі абсцис, його вертикальний піврозмір – похибці по осі ординат. У цьому випадку, якщо одна з помилок – через свою малу величину – не може бути зображена графічно, результати зображають рисочками, які витягнуті на ±Δ в тому напрямі, де похибка немала. Важливість такого способу відображення результатів видно з рис. 3 а, б, де показано одні й ті ж експериментальні точки за різних похибок вимірювань. Графік 3, а безсумнівно, свідчить про нерегулярний хід залежності, яку вивчають. Ця залежність зображена на рис. 3, а кривою лінією. Ті ж дані за великих похибок досліду (див рис.3, б) з успіхом описує пряма лінія, оскільки лише одне вимірювання відступає від кривої більше, ніж на стандартну похибку (і менше, ніж на дві такі похибки). Та обставина, що в разі похибок рис. 3, а дані потребують проведення кривої, а на рис. 3, б цього – ні стає очевидною лише в разі зображення експериментальних результатів у вигляді хрестика похибок. Зі сказаного не випливає, що, зображаючи результати дослідів не хрестиками похибок, а крапками, ми завжди робимо помилку. Якщо значення похибок уже відомі під час побудови графіка, то потрібно, звичайно, їх зображати. Однак переважно ці похибки в момент побудови графіка невідомі і їх треба визначати з розкиду точок на графіку. В таких випадках експериментальні дані ліпше зображати крапками. Лінії, проведені через експериментальні крапки на рис. 3, а і б, не тільки полегшують обстеження даних, а й слугують прикладом опрацювання результатів досліду. Зазначимо, що криві на графіках не завжди проводять через експериментальні точки. Нерідко криві зображають залежність, отриману не з експерименту, а з теоретичних міркувань (чи з інших дослідів). У випадку побудови таких кривих виникає потреба попередньо нанести на графік декілька розрахованих точок. Ці точки треба наносити ледь помітно, щоб не сплутати з чіткими точками (чи хрестиками), які зображають експериментальні дані. Найліпше, щоб розраховані точки взагалі були не помітні.
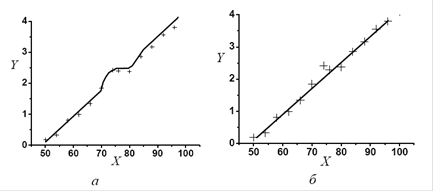
Рис. 3. Проведення кривої через експериментальні точки в разі різних похибок вимірювань. Права частина кривої (а) проведена неправильно – вище експериментальних точок
Осі графіка повинні мати виразні, чіткі позначення. Поряд з поділками на зручних проміжках повинні бути нанесені цифри, які відповідають поділкам шкали. Цифри прийнято розташовувати по краях сітки. На рис. 1, 2 цифри стоять не біля кожної вертикальної лінії, а через одну. На графіках повинно бути позначено, яка фізична величина і в якому масштабі відкладена на осі, як, наприклад, на рис. 1 і 2.
Проведення кривих через експериментальні точки
Через експериментальні точки завжди потрібно проводити найпростішу криву, яка сумісна з цими точками, тобто криву, від якої експериментальні дані відхиляються не більше, ніж на стандартну похибку. Приклад таких кривих зображено на рис. 3. Не потрібно надавати кривим ніяких згинів, якщо експериментальні дані у межах похибок. У разі проведення кривої потрібно стежити за тим, щоб на кожній достатньо великій її ділянці експериментальні точки були розташовані як вище, так і нижче кривої. Наприклад, на рис. 3, а ліва частина кривої проведена правильно, а права – неправильно: жодна з точок не лежить вище цієї кривої. Під час графічного опрацювання результатів потрібно пам’ятати, що “на око” можливо точно провести через експериментальні точки тільки пряму лінію. Тому, будуючи графік, потрібно намагатись, щоб очікувана залежність мала вигляд прямої лінії. Зокрема, вивчаючи залежність в’язкості рідини від температури, маємо право очікувати, що результати описуватиме закон
Якщо відкладати на осях графіка η; і Т, то точки ляжуть на експоненту, яку провести на око майже неможливо. Однак якщо відкладати на осях lnη і 1/ Т, то графік набуде вигляду прямої лінії. Під час вимірювань потрібно завжди старатись, щоб точки на графіку, який потім буде побудований, розташувались достатньо рівномірно. У нашому прикладі для побудови графіка в координатах lnη і 1/ Т потрібно вибирати температуру так, щоб точки лежали на однакових проміжках у шкалі 1/ Т, а не в Т.
|

 .
.
 .
.
 .
.


