Енергія міжмолекулярної взаємодії. Потенціал Ленарда–Джонса
Точну характеристику залежності Е п(r) можна дати лише для конкретних молекул. У загальному
Дослідження доводять, що для молекул рідин і газів достатньо добре наближення отримують за умови n =12, m =6. Тоді, записавши (1.5) через потенціал парної взаємодії φ;(r),отримаємо
де перший доданок відповідає відштовхуванню, а другий – притяганню молекул, σ; – найменша відстань зближення молекул, коли φ;(σ;) = 0. Вираз (1.6) називають потенціалом Леонарда – Джонса. Зазначимо, що формула (1.6) враховує взаємодію лише двох молекул, що можливо тільки для газів. У рідинах треба враховувати вплив сусідніх молекул, що суттєво ускладнює задачу. Водночас потенціал Ленарда–Джонса повністю придатний для наближеної оцінки сил і потенціалу взаємодії. Спробуємо скористатись виразом (1.6), щоб оцінити залежність ван-дер-ваальсівських сил від відстані між молекулами. На підставі рис. 1.3 запишемо напруженість електричного поля, створеного першим диполем на відстані r:
Оскільки
Обчислимо тепер силу, з якою це поле діє на другу поляризовану молекулу:
Оскільки
З урахуванням того, що поляризованість молекули прямо пропорційна до напруженості поля ε, тобто
Отже ван-дер-ваальсівська сила притягування двох молекул дуже швидко зменшується зі збільшенням відстані між ними.
|

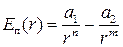 . (1.5)
. (1.5)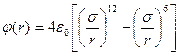 , (1.6)
, (1.6) . (1.7)
. (1.7) і
і 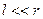 , то
, то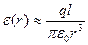 . (1.8)
. (1.8)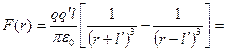
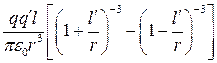 . (1.9)
. (1.9)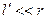 і
і  , то
, то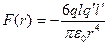 . (1.10)
. (1.10) ~ ε; ~
~ ε; ~ 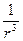 , отримаємо
, отримаємо ~
~  . (1.11)
. (1.11)


