Тиск і температура ідеального газу. Основне рівняння молекулярно-кінетичної теорії
Макропараметри стану газу – тиск р і температуру Т – ми ввели без визначення фізичного змісту цих величин. Щоб з’ясувати їхній фізичний зміст, розглянемо рівняння тиску одноатомного ідеального газу, що його чинить цей газ на стінки посудини. Тиск виникає тому, що під час хаотичного руху кожна молекула газу стикається зі стінками посудини і передає їй імпульс 2 mvx, де vx – складова швидкості, яка перпендикулярна до поверхні стінки. Отже, під час кожного акту взаємодії на стінку діє сила Розглянемо газ як сукупність великої кількості молекул, що рухаються з різними швидкостями, тоді сумарну силу, що діє на стінку, знайдемо шляхом усереднення < F >= За цих умов тиск газу Р = де S – площа стінки, з якою взаємодіють молекули. Зазначимо, що в ідеальному газі молекули мають лише кінетичні енергії теплового хаотичного руху < Е к>= де < V кв> — середня квадратична швидкість молекул газу. На підставі цих міркувань виводять основне рівняння МКТ, тобто рівняння тиску ідеального газу.
де n – концентрація молекул газу, m 0 – маса молекули; Отже, тиск дорівнює двом третім середньої кінетичної енергії поступального руху молекул, що містяться в одиниці об’єму газу. Рівняння (2.10) та (2.11) важливі ще й тому, що пов’язують макропараметр стану газу (тиск р) з масою, швидкістю та енергією окремих молекул. Порівняємо основне рівняння МКТ (2.11) з рівнянням стану одноатомного ідеального газу (2.7) й отримаємо < Е к>= Як бачимо, середня кінетична енергія поступального руху молекули ідеального газу прямопропорційна до його абсолютної температури. Отже, абсолютна температура є мірою середньої кінетичної енергії молекул газу. Важливо, що (2.12) не містить ніяких характеристик молекул, а це означає, що за сталої температури середні кінетичні енергії молекул будь-яких газів, у тім числі складових суміші, є однаковими, а < Е к> не залежить від типу газу. З рівняння (2.12) можна легко отримати вираз для середньої квадратичної швидкості молекул. Оскільки < Е к>=
|

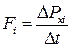 .
.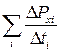 . (2.8)
. (2.8)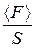 , (2.9)
, (2.9)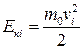 . Ці енергії не однакові для різних молекул, оскільки під час зіткнень їхні швидкості змінюються і за напрямом, і за значенням. На практиці використовують середню кінетичну енергію молекули
. Ці енергії не однакові для різних молекул, оскільки під час зіткнень їхні швидкості змінюються і за напрямом, і за значенням. На практиці використовують середню кінетичну енергію молекули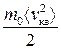 , (2.10)
, (2.10)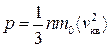 , або
, або 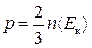 , (2.11)
, (2.11)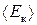 – середня кінетична енергія поступального руху молекули.
– середня кінетична енергія поступального руху молекули.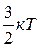 . (2.12)
. (2.12)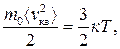 то < v кв>=
то < v кв>= 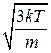 =
= 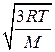 =
= 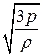 . (2.13)
. (2.13)


