Поняття про статистичний розподіл. Функції розподілу
2.3.1. Закони розподілу молекул ідеального газу за швидкостями й енергіями теплового руху (розподіл Максвелла) Під час хаотичного руху молекули ідеального газу зазнають багаторазових зіткнень, унаслідок чого змінюються і значення, і напрям їхніх швидкостей. Водночас, як з’ясовано вище, середня квадратична швидкість молекул < v кв> за умови Т =const є сталою. Це можна пояснити тим, що в газі, який перебуває у рівноважному стані, усталюється певний розподіл молекул за швидкостями. Дж. Максвелл на підставі закономірностей математичної статистики і теорії імовірності вивів закон цього розподілу: f (v)= де N – кількість молекул газу; dN (v) – кількість молекул, швидкість яких є в проміжку від v до v + dv. Розподіл Максвелла описує деяка функція f (v) – функція розподілу молекул за швидкостями, або густина імовірності того, що молекула має швидкість v. Функція f (v) dv визначає відносну кількість молекул газу, швидкість яких є у проміжку від v до v + dv. Умова нормування функції f (v)
Графік функції розподілу f (v) показано на рис. 2.4. Характерний вигляд графіка f (v) зумовлений добутком Максимум функції f (v) відповідає найімовірнішій швидкості молекул v і, яку можна знайти шляхом диференціювання (2.14):
звідки Зазначимо, що з підвищенням температури максимум функції зсувається в бік більших швидкостей, однак площа під ним є сталою (див. рис. 2.4). Якщо функція розподілу f (v) відома, то з рівняння (2.14) можна визначити відносну кількість молекул газу, швидкість яких є в заданому проміжку швидкостей v 1, v 2:
Оскільки f (v) є густиною імовірності, то можна знайти середнє значення будь-якої функції j (v):
Скористаємось (2.19), щоб знайти середню арифметичну < v > та середню квадратичну <
Як бачимо, вирази для < Середню арифметичну, найімовірнішу та середню квадратичну швидкості називають характерними швидкостями розподілу Максвелла. Кінетична енергія молекул залежить від їхньої швидкості, тому на підставі (2.14) можна знайти розподіл молекул за їхніми кінетичними енергіями. Зробимо у (2.14) заміну змінних:
Тоді із (2.13), (2.14) і (2.22) отримаємо
Функція
є функцією розподілу молекул за енергією теплового руху.
|

 (2.14)
(2.14) (2.15)
(2.15) що очевидно, оскільки імовірність того, що молекула має швидкість у проміжку від 0 до ¥, дорівнює одиниці.
що очевидно, оскільки імовірність того, що молекула має швидкість у проміжку від 0 до ¥, дорівнює одиниці.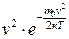 . За малих швид-костей множник v 2 у рівнянні (2.14) зростає швидше, ніж спадає
. За малих швид-костей множник v 2 у рівнянні (2.14) зростає швидше, ніж спадає 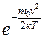 , а за великих швидкостей переважає експонента.
, а за великих швидкостей переважає експонента. , (2.16)
, (2.16) . (2.17)
. (2.17) . (2.18)
. (2.18) . (2.19)
. (2.19) > швидкості молекул газу:
> швидкості молекул газу: (2.20)
(2.20) . (2.21)
. (2.21) , звідки
, звідки  , а
, а  . (2.22)
. (2.22) . (2.23)
. (2.23) (2.24)
(2.24)


