Середня кількість зіткнень молекул. Середня довжина вільного пробігу
Під час зіткнень від-стань між молекулами стає мінімальною. Цю відстань називають ефективним газокінетичним діаметром молекули d (рис. 2.6). Величина s=p d 2 – це ефективний поперечний переріз молекули. Зіткнення – це ймовірнісний процес. Обчислимо ймовірність зіткнення молекули з іншою з таких міркувань. Нехай молекула А рухається вздовж Ох і потрапляє в об’єм dV=Sdx, у якому містяться інші молекули (умовно їх уважатимемо нерухомими). Кількість молекул у цьому об’ємі dN=n 0 Sdx. (2.37) Сумарна площа перерізу цих молекул dS=sdN= s n 0 Sdx. (2.38) Тоді ймовірність зіткнень молекули А з молекулою в об’ємі dV dw= у цьому разі w= s n 0 x. За умови x >> < l > імовірність зіткнення дорівнює одиниці, отже,s n 0< l >=1, звідки
Як бачимо, середня довжина вільного пробігу – це шлях, на якому ймовірність зіткнення дорівнює одиниці. Обчислимо тепер середню кількість зіткнень молекули за одиницю часу. Очевидно, що за час D t молекула проходить шлях
де
Досі ми вважали, що рухається лише одна молекула, а інші – нерухомі. З урахуванням руху інших молекул отримаємо
За допомогою рівняння стану газу р=nkT можна довести, що
Отже, з підвищенням тиску кількість зіткнень зростає, а довжина вільного пробігу зменшується.
|

 Хаотичний рух молекул газу супроводжується їхніми зіткненнями. Протягом проміжку часу D t між двома послідовними зіткненнями молекула проходить певний відрізок шляху l, який називають довжиною вільного пробігу. Очевидно, що за великої кількості зіткнень, яких зазнає молекула, зна-чення l є різним, тому вводять поняття < l > середньої довжи-ни вільного пробігу.
Хаотичний рух молекул газу супроводжується їхніми зіткненнями. Протягом проміжку часу D t між двома послідовними зіткненнями молекула проходить певний відрізок шляху l, який називають довжиною вільного пробігу. Очевидно, що за великої кількості зіткнень, яких зазнає молекула, зна-чення l є різним, тому вводять поняття < l > середньої довжи-ни вільного пробігу.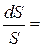 s n 0 dx, (2.39)
s n 0 dx, (2.39) . (2.40)
. (2.40) (2.41)
(2.41) – середня швидкість поступального руху молекули; Z – кількість зіткнень. Тоді за 1 с молекула зазнає
– середня швидкість поступального руху молекули; Z – кількість зіткнень. Тоді за 1 с молекула зазнає 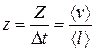 зіткнень або, на підставі (2.41),
зіткнень або, на підставі (2.41),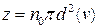 . (2.42)
. (2.42) (2.43)
(2.43)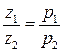 або
або  . (2.44)
. (2.44)


