Для ізобарного процесу
Класична теорія добре описує теплоємність одноатомних газів. Зокрема, ізохорна теплоємність інертних газів (Не, Аr, Xe, Kr), за даними експерименту, справді становить 3/2 R і не залежить від температури. Водночас теплоємність двохатомних газів виявляє залежність від температури (рис. 3.1). Цю невідповідність класичної теорії та експерименту пояснює квантова теорія теплоємності, згідно з якою для енергії обертального та коливального рухів складних молекул характерний дискретний спектр:
де ν; – частота коливань атомів у молекулі; J 0 – момент інерції молекули; ħ;
Для водню ці температури становлять 85,5 і 5 410 К, відповідно. З погляду квантової теорії ізохорна теплоємність двохатомного газу
За умови hν;>> kТ вираз (3.16) перетворюється в класичний
|
. (3.13)
Це рівняння Майєра, яке свідчить, що ізохорна й ізобарна молярні теплоємності ідеального газу є різними.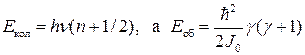
, (3.14)
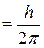– стала Планка; n =0,1,2,3... i j =0,1,2,3... – квантові числа. У квантовій теорії замість статистики Максвелла–Больцмана використовують статистику Бозе–Айнштайна. На підставі (3.14) можна визначити температури, за яких збуджуються коливальні й обертальні ступені вільності молекул:
. (3.15)
. (3.16)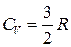
. Отже, квантова теорія повніше описує теплоємність ідеального газу.
