Вище доведено, що середня кінетична енергія теплового руху молекули ідеального газу
Однак зазначимо, що рівняння (3.4) справджується тільки для одноатомних молекул. У випадку багатоатомних молекул необхідно враховувати їхнє число ступенів вільності і. Числом ступенів вільності системи називають кількість незалежних змінних, які однозначно визначають її енергетичний стан. Якщо деяку частинку розглядати як матеріальну точку в потенціальному полі, то її повна енергія Е = Е к+ Е п залежить від компонент швидкості vx, vy, vz i координат x, y, z. Отже, для такої частинки і =6. Молекули ідеального газу можуть бути одно-(Ar, Kr, Ne) і багатоатомними (О2, H2, H2O, CO2, CH4). Повна енергія одноатомної молекули визначена лише кінетичною енергією її поступального руху, оскільки Е п=0. Отже, для одноатомних молекул ідеального газу і = і пост=3. Для багатоатомних молекул, крім енергії поступального руху, характерна також енергія обертального та коливального рухів (нежорсткі молекули) навколо спільного центра мас. З огляду на це в разі розрахунку числа ступенів вільності багатоатомних молекул необхідно враховувати, поряд з поступальним рухом молекули як цілого, обертальний та можливий коливальний рух молекул. Згідно з теоремою Больцмана, енергія рівномірно розподіляється за ступенями вільності. В системі, яка перебуває в стані термодинамічної рівноваги, на кожен поступальний і обертальний ступінь вільності припадає енергія kT /2, а на кожен коливальний ступінь вільності – kT. Отже, повне число ступенів вільності молекули і = і пост+ і об+2 і кол. Тоді
З урахуванням (3.3) і (3.5) внутрішню енергію U ідеального газу виразимо так:
або
де n – кількість молів газу.
|

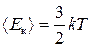 . (3.4)
. (3.4)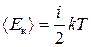 . (3.5)
. (3.5) (3.6)
(3.6)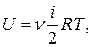 (3.7)
(3.7)


