Распределение Максвелла. Назовем состояние газа равновесным,если параметры состояния газа при отсутствии внешних воздействий остаются неизменными во времени.
Назовем состояние газа равновесным,если параметры состояния газа при отсутствии внешних воздействий остаются неизменными во времени. Пусть газ находится в равновесном состоянии при температуре Определим вероятность того, что модуль скорости молекулы лежит между
(17. 1) Введем величину
(17. 2) плотность вероятности, которая является функцией модуля скорости молекулы, в связи с чем её называют функцией распределения вероятности молекул по скорости или просто функцией распределения молекул по скоростям. Комбинируя формулы (17. 1) и (17. 2), получаем
(17. 3) откуда
Зная вид функции Максвелл теоретически получил вид функции распределения молекул по скоростям:
(17. 5) где
Изобразим график функции (17. 5) (рис. 17. 1).
Рис. 17. 1
Из графика видно, что вероятность обнаружения в газе молекулы со скоростью, лежащей в интервале от
равна заштрихованной площади под кривой Вероятность обнаружения в газе молекул с любой скоростью от 0 до
(17. 6) т. е. площадь под всей кривой Скорость, соответствующая максимуму функции распрделения Для
Продифференцируем выражение (17. 5) по
При -
откуда
Откуда получаем
(17.7) Используя функцию распределения (17. 5), можно найти среднюю
(17. 8)
|

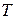 . Молекулы газа, непрерывно сталкиваясь между собой, меняют свои скорости, как по направлению, так и по величине. Мы не можем сказать, с какой скоростью станет двигаться произвольно выбранная молекула в той или иной момент времени. В то же самое время мы можем говорить о некотором стационарном (устойчивом) распределении молекул по скоростям: одни молекулы движутся быстро, другие медленно. Но на всякий интервал скоростей, например, от 10 до 20 м/с или от 20 м/с до 30 м/с, будет приходить в среднем (по времени) некоторое определенное число молекул. При отсутствии внешних воздействий установившееся при данной температуре распределение молекул по скоростям в дальнейшем не изменяется.
. Молекулы газа, непрерывно сталкиваясь между собой, меняют свои скорости, как по направлению, так и по величине. Мы не можем сказать, с какой скоростью станет двигаться произвольно выбранная молекула в той или иной момент времени. В то же самое время мы можем говорить о некотором стационарном (устойчивом) распределении молекул по скоростям: одни молекулы движутся быстро, другие медленно. Но на всякий интервал скоростей, например, от 10 до 20 м/с или от 20 м/с до 30 м/с, будет приходить в среднем (по времени) некоторое определенное число молекул. При отсутствии внешних воздействий установившееся при данной температуре распределение молекул по скоростям в дальнейшем не изменяется. и
и  . Пусть
. Пусть  - общее число молекул в еденице объема газа, а
- общее число молекул в еденице объема газа, а  - число молекул в еденице объема газа, скорости которых лежат между
- число молекул в еденице объема газа, скорости которых лежат между 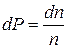
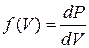
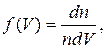
 (17. 4)
(17. 4)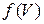 , можно, интегрируя выражение (17. 4), определить количество молекул в еденице объема газа, скорости которых лежат в любом интервале скоростей.
, можно, интегрируя выражение (17. 4), определить количество молекул в еденице объема газа, скорости которых лежат в любом интервале скоростей.
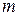 и
и  - постоянная Больцмана.
- постоянная Больцмана.
 до
до 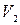 (см. формулу (17. 2)).
(см. формулу (17. 2)).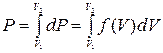

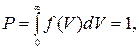
 скоростью молекул. Найдем эту скорость.
скоростью молекул. Найдем эту скорость. очевидно
очевидно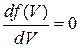 .
.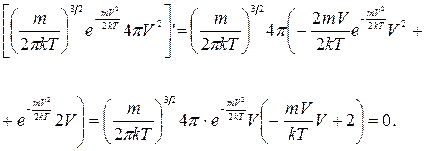
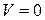 и
и 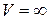 функция
функция 

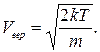
 и среднюю квадратную
и среднюю квадратную  скорости молекул:
скорости молекул:
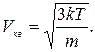 (17. 9)
(17. 9)


