Основное уравнение молекулярно-кинетической теории
Как было установлено, основной характеристикой внутреннего состояния любых систем (твердых, жидких или газообразных), состоящих из достаточно большого числа частиц-молекул, является температура. Такие системы, основной характеристикой внутреннего состояния которых является температура, называются термодинамическими. С другой стороны, простейшей (не равной нулю) характеристикой молекулярного движения является средний квадрат скорости Более привычной величиной, содержащей эту характеристику, является средняя кинетическая энергия молекулы или просто кинетическая энергия.
Очевидно, что m 0 — масса одной молекулы. Разумно предположить, что температура и средняя энергия молекулярного движения — внутренняя энергия, приходящаяся на одну молекулу, должны быть связаны между собой. Эта связь Чтобы установить эту связь, вспомним, что температура связана с другими характеристиками газа уравнением состояния или
Параметры: р — давление, V — объем, ν — количество вещества (в молях), наряду с температурой, являются характеристиками газа в целом. Такие характеристики называются макроскопическими — «большими». С другой стороны, такие величины, как масса одной молекулы т 0; скорость
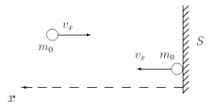
Оказывается, что легче всего связать с микроскопическими характеристиками давление. С одной стороны, давление р = F / S, т. е. сила, действующая со стороны газа на единицу площади S поверхности стенок сосуда, окружающего газ. С другой стороны, очевидно, что сила действия газа на стенку возникает из-за ударов молекул (рис. 1.14).
Рис. 1.14. Удар молекулы о стенку, перпендикулярно направленную ее движению Найти: р —? Дано: m 0; V 2; N; V.
|

 .
. (1.34)
(1.34) и Т имеет самый простой — простейший вид. Оказывается, что средняя энергия хаотического движения молекул (бывает и направленное — «ветер») газа прямо пропорциональна температуре. Весь дальнейший длинный вывод нужен для определения коэффициента пропорциональности. Попутно, однако, выявляется много нового. Итак, в путь!
и Т имеет самый простой — простейший вид. Оказывается, что средняя энергия хаотического движения молекул (бывает и направленное — «ветер») газа прямо пропорциональна температуре. Весь дальнейший длинный вывод нужен для определения коэффициента пропорциональности. Попутно, однако, выявляется много нового. Итак, в путь!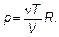 (1.35)
(1.35)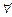 (Vx; Vу; Vz), следовательно, квадрат скорости V 2, являются характеристикой одной молекулы, и их, естественно, называют микроскопическими. Выпишем:
(Vx; Vу; Vz), следовательно, квадрат скорости V 2, являются характеристикой одной молекулы, и их, естественно, называют микроскопическими. Выпишем: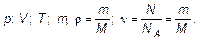
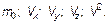
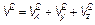 .
.