Решение. где F — сила действия всех N молекул.
где F — сила действия всех N молекул. Силу действия всех молекул F можно выразить через силу действия на стенку одной молекулы f. Запишем:
где Z — число ударов молекул о стенку площадью S за время t. Знак усреднения в этой формуле необходим. Прибор, измеряющий давления, сам (будучи макроскопическим — «большим») производит усреднение. Если бы была возможность поставить прибор, который регистрировал бы «каждый» удар отдельно, то на графике зависимости давления от времени появилась бы «мелкозубая пила» (рис. 1.15).
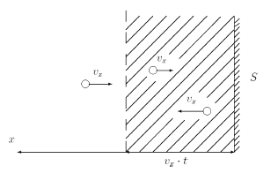
Рис. 1.15. Превращение микроскопической характеристики в макроскопическую В действительности прибор не успевает столь быстро реагировать. С другой стороны, характеристики «зубчиков» никого не интересуют. Поэтому давление — среднее значение. Перефразируя Григория Сковороду, скажем: «Сложное — не нужно, а ненужное — сложно». Впрочем, не все с этим согласны. Перейдем к вычислению числа Z ударов молекул о стенку за время t. Соударение со стенкой испытают все молекулы, которые за время t успеют долететь до стенки. Долететь же они успеют с расстояния Vxt, т. к. движение можно считать равномерным. (Сил взаимодействия во время движения нет — это одно из приближений идеального газа, см. рис. 1.12.) С большего расстояния молекулы не успевают долететь до стенки. Объем, из которого молекулы долетают до стенки (рис. 1.16), равен VxtS (произведение длины Vxt на площадь S). В этом объеме находятся nVxtS молекул; произведение концентрацииn = N / V молекул на только что подсчитанный объем, из которого молекулы долетают до стенки.
Рис. 1.16. К вычислению числа молекул, сталкивающихся со стенкой. Однако о стенку ударит только половина этого числа. Другая половина имеет Vx компоненту скорости, направленную от стенки, и летит в противоположном направлении. Итак,
Теперь вычислим силу действия одной молекулы, которая, имея скорость Vx, ударяет о стенки. Прежде всего, отметим, что для анализа движения такой молекулы будет применяться механика Ньютона. Для столь малого объекта, как молекула, применимость механики требует оговорки, ведь установлена механика Ньютона (классическая механика) на основе рассмотрения движения макроскопических тел. Считается, что в идеальном газе, где молекулы рассматриваются, как малые шарики, такое приближение применимо. Кроме того, принимают, что в идеальном газе взаимодействие на малых расстояниях считается бесконечно сильным, упругим (см. п. 2.6). Удобно вообще не анализировать, «что там происходит при ударе молекулы о стенку», а учесть изменение импульса:
как разность импульса в конечном состоянии m 0 Vх (после удара) и импульса в начальном состоянии (до удара) т 0 V 0 x. «Упругость» проявляется в том, что начальная и конечная скорости равны по величине, но противоположны по направлению: V 0 x = – Vx. Тогда сила удара молекулы о стенку будет
Вычисляем силу действия всех молекул газа на стенку:
Видим, что время t сократилось, значит, сила действия молекул газа на стенку постоянная. Все величины в формуле силы постоянные, кроме скорости Vx. Как и следовало ожидать, в макроскопическую характеристику, силу, вошел средний квадрат скорости движения молекулы. Как уже указывалось (см. рис. 1.13), средний квадрат скоростей молекул в любой момент времени равен среднему квадрату скорости одной молекулы за достаточно длительное время. Это утверждение, как уже указывалось, называется эргодической гипотезой. Принимаем эту гипотезу. Она верна! До сих пор рассматривались молекулы со скоростями, параллельными оси x. Реально, конечно, молекулы могут иметь произвольно направленные скорости (рис. 1.17).
Рис. 1.17. Скорость в пространстве Введение осей — дело рук человеческих. Молекулы «не знают», как мы провели и обозначили оси. Можно было, например, направить ось x, как y, a y — как x. Поэтому хаотичность движения проявляется в том, что в среднем:
Нужная нам проекция:
Тогда давление на стенку будет
Обратим внимание на правильность чтения. Например, Так как давление зависит от скорости (пусть от среднего квадрата скорости), то сила давления pS — не консервативна, т. е. работа этой силы зависит от способа (от пути), которым совершается эта работа. Итак, давление прямо пропорционально среднему квадрату скорости. Теперь можно записать и результат — основное уравнение молекулярно-кинетической теории газа:
где, вспомним,
Главный результат можно сформулировать так: давление пропорционально средней энергии молекул газа и концентрации этого газа.
Учет реальности газа, такой как учет собственного объема молекул или парных взаимодействий, не изменит того, что произведение pV (может быть несколько измененное) пропорционально энергии молекул газа.
|

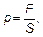 (1.36)
(1.36)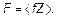 (1.37)
(1.37)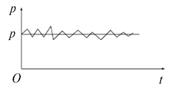
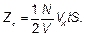 (1.38)
(1.38)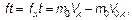 (1.39)
(1.39) (1.40)
(1.40)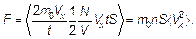 (1.41)
(1.41)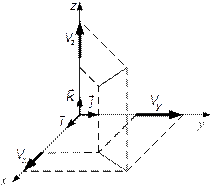
 (1.42)
(1.42) (1.43)
(1.43) (1.44)
(1.44)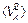 читается «средний квадрат проекции скорости на ось х». Прочесть «квадрат средней скорости» — неверно! Квадрат средней проекции скорости
читается «средний квадрат проекции скорости на ось х». Прочесть «квадрат средней скорости» — неверно! Квадрат средней проекции скорости  равен нулю.
равен нулю. (1.45)
(1.45)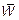 — средняя кинетическая энергия молекулы идеального газа,
— средняя кинетическая энергия молекулы идеального газа,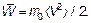 (1.46)
(1.46)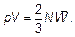 (1.47)
(1.47)


