Энтропия. Анализ изотермического процесса показывает, что теплота может выделяться (или поглощаться) и без изменения температуры
Анализ изотермического процесса показывает, что теплота может выделяться (или поглощаться) и без изменения температуры, поэтому запись изменения теплоты в виде, пропорциональном изменению температуры δ Q = С Δ Т, по крайней мере, не универсальна. Кроме того, записав приращение теплоты как δ Q = dU + pdV, (2.20) что прямо следует из первого начала, можно заметить: справа стоят такие величины, значения которых для тела в целом, например в изобарном процессе, равны сумме значений тех же величин для отдельных частей этого тела. В самом деле, энергия целого равна сумме энергий частей, объем целого также равен сумме объемов частей. Температура, очевидно, таким свойством не обладает. Если сложить две части тела, одну нагретую до 340 К (нагретую воду), а другую нагретую до 310 К (палец), то вместе они нагревания до 650 К не дадут. С другой стороны, теплота δ Q соответствует (например, в изохорном процессе) изменению энергии dU, а температура Т — средней энергии, поэтому отношение δ Q / T должно определяться числом состояний, в которых могут быть такие «средние» энергии. Итак, введем формально величину S, называемую энтропией, по формуле
По своему смыслу энтропия должна быть связана с числом возможныхсостояний энергии в теле. Число возможных состояний энергии, очевидно, связано «просто» с числом возможных сочетаний Γчастей той или иной системы. Число сочетаний определяется числом частиц-молекул и их энергетическими состояниями, например уровнями энергии. Оказывается, что S = k ;ln Γ. (2.22) Эта формула была открыта Больцманом, и k — все та же постоянная Больцмана: k = R / NA = 1,4 ⋅ 10–23 Дж/К. (По размерности подходит!) Теперь от рассуждений перейдем к вычислениям, и тогда, может быть, станет яснее. Вычислим энтропию идеального газа. Это система, удовлетворяющая уравнению состояния р / Т = ν R / V и имеющая внутреннюю энергию U = сV ν T. Из первого начала:
Интегрируя (причем помня, что интеграл дает логарифм), получим:
Из этой формулы видно, что энтропия — функция состояния, т. е. каждому состоянию газа соответствует определенная энтропия (как, например, внутренняя энергия U). Как и многие другие величины в физике (например, потенциал да и потенциальная энергия), энтропия определена лишь с точностью до постоянной — постоянной S 0 — значения энтропии, определяемой особо. Определение S 0выходит за рамки этого курса. Практически важно знать только разность энтропий. Так обстоит и, например, с потенциалом электрического поля, важна лишь разность потенциалов Δφ, определяющая напряжение U. Вычислим разность энтропий двух состояний (разность логарифмов свернется в частное):
Теперь легко получить формулы для изменения энтропии в различных, изученных ранее изопроцессах. Найдем изменение энтропии в изотермическом процессе (при T 2/ T 1 = 1):
Изменение энтропии в изохорном процессе (при V 2/ V 1=1):
Изменение энтропии в изобарном процессе, когда по закону Гей-Люссака V 2/ V 1 = T 2/ T 1, подставив, увидим, что
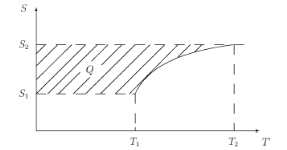
Здесь использовано, что по закону Майера теплоемкость при постоянном давлении (изобарная) равна сp = сV + R. На диаграмме S – T (рис. 2.5), учитывая, что cp > cV, изобара пройдет выше изохоры при одинаковых исходных состояниях. На такой диаграмме (рис. 2.6) теплота — это площадь между кривой и осью энтропии.
Рис. 2.5. Диаграмма S – T: (1) — изобара; (2) — изохора
Рис. 2.6. Теплота на диаграмме S – Т Наконец, изменение энтропии в адиабатном процессе (при dQ =0), очевидно,
Итак, в адиабатном процессе энтропия не изменяется. Часто именно это положение используют как определение адиабатного процесса. Легко увидеть, что формула (2.29) есть просто другая запись закона адиабатного процесса. Сокращая ν сV и «загоняя» все под логарифм (в показатель степени), а затем опуская логарифм, получим:
Это соотношение с помощью уравнения состояния преобразуется в
Получился уже выведенный ранее закон и постоянная Пуассона, равная γ = cp / cV.
|

 (2.21)
(2.21)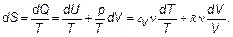 (2.23)
(2.23) (2.24)
(2.24)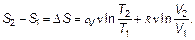 (2.25)
(2.25) (2.26)
(2.26)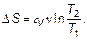 (2.27)
(2.27)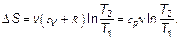 (2.28)
(2.28)
 (2.29)
(2.29) (2.30)
(2.30) (2.31)
(2.31)


