Распределение молекул по скоростям
Так как тепловое движение — хаотическое (беспорядочное), то скорости молекул имеют всевозможные случайные значения, различающиеся по величине и направлению (имеют всевозможные проекции, например, на ось х). До сих пор удавалось обходиться среднеквадратичной скоростью, главное свойство которой заключалось в том, что кинетическая энергия, пропорциональная среднему квадрату скорости á V 2ñ, сама прямо пропорциональна температуре Т. Для одной молекулы (массой т 0) двухатомного газа
где
Напомним, эта величина называется постоянной Больцмана. Отсюда среднеквадратичная скорость молекулярного движения
прямо пропорциональна корню квадратному из температуры и обратно пропорциональна корню квадратному из молярной массы газа. Если необходимо характеризовать скорости молекул (или другие их характеристики) более подробно, то нужно использовать методы статистики. Статистика — наука о качественных характеристиках массовых объектов (здесь молекул), имеющих случайные свойства. Основные методы статистики — это методы теории вероятностей. В основе слова «статистика» (statistics) можно увидеть корень «state» (штат, государство). Массовые явления нужно анализировать, чтобы понимать процессы в государстве. Существует огромная область физики и химии — статистическая физика. Здесь будут рассмотрены лишь отдельные элементы этой науки. Итак, удобно молекулы разделить на группы с близкими скоростями — скоростями, лежащими в интервале от V до dV. Всего молекул в газе N, а молекул со скоростями в заданном интервале будет dN. Так как молекул «много», то и N — велико, и dN — велико. Поэтому удобно характеризовать тепловое движение «долей» молекул, имеющих скорости от V до Δ V. Такая доля dN / N — это отношение числа молекул, имеющих скорость, близкую к требуемой, к общему числу молекул. Очевидно, что чем больше интервал скоростей dV ≈ Δ V, в который входят молекулы из dN ≈ Δ N, тем и само число молекул со скоростями в этом интервале dN тоже больше. Короче, доля Δ N / N прямо пропорциональна Δ V — интервалу скоростей. Коэффициент пропорциональности между долей молекул газа dN / N, имеющих скорость, близкую к какой-то (любой, но одной) скорости V и интервалом скоростей Δ V, в котором скорости считаются «близкими», зависит уже только от самой этой избранной скорости, обозначается F (V) и называется функцией распределения.
Конечно, функцией распределения можно характеризовать не только величины (модули) скоростей, но и, например, проекции скорости на любую ось (назовем ее осью x):
Функции распределения различных величин — характеристик множества молекул, несколько различаются, но в главном они одинаковы. Мало молекул с «крайними» характеристиками. Мало очень «быстрых» и мало очень «медленных». Вот с какими-то «средними» значениями скорости (модуля скорости) молекул будет «много» (рис. 3.2).
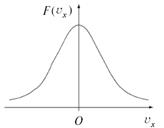
Рис. 3.2. Распределение молекул по скоростям (по величинам скоростей) Также и молекул, быстро летящих вдоль оси x как в положительном, так и в отрицательном направлении, будет немного, а молекул с малыми проекциями скоростей (т. е. с большими проекциями на другие оси) гораздо больше (рис. 3.3).
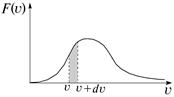
Рис. 3.3. Распределение молекул по проекциям скорости Такой вид функций распределения подтверждается на опыте. Рассмотрим физический смысл функции распределения F (V). Пусть газ содержит N молекул. Найдем число молекул dN, скорости которых имеют значение от V до V + dV. Очевидно, площадь, закрашенная на рис. 3.4, есть вероятность обнаружения таких молекул, т. е. их относительное число dN / N.
Рис. 3.4. Физический смысл функции распределения Максвелла: закрашенная площадь — доля молекул со скоростями от V до V + dV Поскольку величина закрашенной площади равна F (V) dV,то
Таким образом, число молекул со скоростями в интервале (V, V + dV) равно dN = NF (V) dV. (3.9)
|

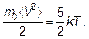 (3.3)
(3.3)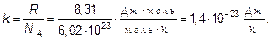 (3.4)
(3.4)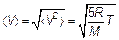 (3.5)
(3.5)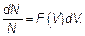 (3.6)
(3.6)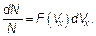 (3.7)
(3.7)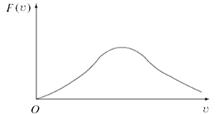
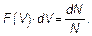 (3.8)
(3.8)


