Распределение Больцмана. Вернемся к физике — к молекулярно-кинетической теории
Вернемся к физике — к молекулярно-кинетической теории. В статистической физике есть свой главный закон, закон-«генерал». Этот закон был сформулирован Людвигом Больцманом в конце XIX в. и называется распределением Больцмана. Часто этот закон называют также принципом Больцмана. Больцман знал, что к молекулярной физике нужно применить методы теории вероятностей. С другой стороны, он был физиком и понимал, что главной характеристикой любого состояния молекул, множества, ансамбля молекул должна являться их энергия. Как известно (см. гл. 1), естественной мерой энергии молекулярного движения — внутренней энергии — является температураТ. Безразмерной характеристикой любого состояния всех молекул (частиц), сразу ясно, будет тогда величина W /(kT) где k — уже знакомая нам величина k = 1,4 ⋅ 10–23Дж/К — постоянная Больцмана. Главное достижение Больцмана заключалось в том, что он понял: чем меньше энергия, тем число состояний с такой энергией больше. Вероятность, что ансамбль молекул имеет какую-то энергию, тем меньше, чем эта энергия больше. Теория же вероятностей подсказала ему, что степень этого уменьшения определяется экспоненциальным законом. По принципу (распределению) Больцмана число состояний с энергией W, а потому и вероятность реализации такого состояния пропорциональна:
Например, концентрация всегда равна
В такой зависимости счастливо сочетаются свойства, во-первых, свойство энергии — то, что энергия вычисляется как сумма отдельных частиц, отдельных видов (потенциальная и кинетическая энергия, например) и отдельных взаимодействий (гравитационный и электрический, например), и, во-вторых, свойство экспоненты, которая есть произведение экспонент с отдельными слагаемыми энергии в показателе каждого сомножителя. Поэтому в показатель экспоненты можно выделить исследуемую зависимость, а все остальное считать заключенным в коэффициенте пропорциональности — каждый раз разном. Проиллюстрируем эти «туманные» рассуждения на примерах. 3.4.1. Распределения молекул Энергия взаимодействия молекулы с полем притяжения Земли W = m 0 gh. Поэтому распределения молекул в атмосфере под действием силы тяжести в соответствии с принципом Больцмана запишется как:
В начальную концентрацию, концентрацию п 0, на поверхности Земли (на «уровне моря») отнесены все другие факторы, возможно, влияющие на молекулы. Эта формула часто называется барометрической. Она связала высоту h над некоторым нулевым уровнем и давление, которое при постоянной температуре прямо пропорционально концентрации. Переходя к молярной массе М / R = т 0/ k, получим
График распределения молекул в атмосфере под действием силы тяжести, построенный в соответствии с принципом Больцмана, представлен на рис. 3.8.
Рис. 3.8. Распределение молекул в атмосфере под действием силы тяжести. Представлена зависимость концентрации n от высоты над уровнем Земли h
|

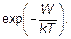 (3.19)
(3.19) (3.20)
(3.20) (3.21)
(3.21) (3.22)
(3.22)



