Барометрическая формула. Барометрическая формула(3.22) уже была получена «даром» из принципа Больцмана

Барометрическая формула (3.22) уже была получена «даром» из принципа Больцмана. Сейчас мы получим эту же формулу, не используя распределение Больцмана, и тем самым покажем, как ценно знать общие законы.

Известно, что давление жидкости или газа определяется высотой столба жидкости (газа) Δ р = ρ gh, где ρ — плотность газа. Однако определить по этой формуле давление можно только, если плотность газа от давления не зависит. При большой высоте это, конечно, не верно. При малом же столбе dh формула верна, но она определяет тогда лишь малое изменение давления dp. Итак:

dp = –ρ gdh. (3.43)

Вот теперь, используя уравнения состояния идеального газа, исключим плотность из уравнения состояния р = ρ M / RT и получим дифференциальное уравнение. Знак «минус» показывает, что с высотой давление убывает, ведь давление определяется направлением силы, а сила, как видно на рис. 3.17, направлена противоположно оси. Разделяя переменные, получим дифференциальное уравнение в виде, удобном для интегрирования. Запишем

(3.44)

Интегрируем

(3.45)

где р 0 — давление на том уровне, который выбран за начало отсчета высоты (уровень моря). Получим ln p – ln p 0 = Mgh / RT.

Потенцируя, находим барометрическую формулу

(3.46)

которая, конечно, «не знает», как мы ее находим, но «знает», как газ распределяется по высоте при одинаковой температуре (рис. 3.18).

Рис.3.17. К выводу барометрической формулы

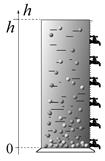
Рис.3.18. Зависимость давления в атмосфере от высоты при постоянной температуре

Барометрическая формула лежит в основе метода седиментации (оседания), позволяющего определять молярные массы больших молекул или коллоидных частиц. Для этого определяют под микроскопом концентрации таких молекул (частиц) в равновесном достаточно высоком столбе жидкости (рис. 3.19). Метод основан на выявлении характерного масштаба h a(высота однородной атмосферы), присущего оседанию именно исследуемых частиц (молекул).

Рис. 3.19. Цилиндр для опытов по седиментации

Безразмерным числом является показатель экспоненты Мgh /(RT). Отсюда следует, что выражение

(3.47)

имеет размерность длины — метр (м) — и с полным основанием может рассматриваться как характерная длина, т. е. такая длина (разность высот), на которой существенно меняется давление из-за действия на молекулярное движение сил тяжести.

По данным эксперимента (рис. 3.20) строят график зависимости

(3.48)

По этому графику, как отношение противолежащего катета к прилежащему, определяют тангенс угла наклона tgα. Как неоднократно указывалось (см., например, п. 1.1 в самом начале курса) тангенс угла наклона касательной к графику (здесь — прямая) с осью абсцисс равен производной. Поэтому tgα = 1/ h a. Затем по формуле М = RT /(gh a) определяют молярную массу.

Рис. 3.20. График (градуировочная кривая) для определения молярной массы методом седиментации

Чувствительность опытов по седиментации можно существенно увеличить, поместив кювету («столб») с жидкой взвесью в центрифугу. Тогда ускорение силы тяжести g ≈ 9,8 Н/кг может быть заменено гораздо большей величиной центростремительного ускорения ω² R. Угловая скорость ω у центрифуги велика, и хотя расстояние R от оси вращения до места в кювете, где определяется концентрация, как правило, гораздо меньше h, все равно энергия М ω² R ² >> Mgh. Все формулы, описывающие оседание в поле тяжести, переписываются для оседания в центрифуге, если заменить величину gh на ω² R ².