Наиболее вероятная скорость. Метод анализа размерностей
Перейдем к исследованию и анализу полученной функции распределение Максвелла (3.30). Найдем положение максимума, т. е. такую скорость, которую имеет наибольшая доля (или число) молекул при равных интервалах разделения молекул по скоростям (один и тот же интервал dV). Вычисляем производную и приравниваем ее к нулю: dF (V)/ dV = 0, или
Производная берется по формуле производной от произведения. Производная от экспоненты берется как производная «сложной» функции. Постоянная величина, не зависящая от скорости, сокращена. Сокращая последнюю формулу на V и на экспоненту, получим, что скорость, которой соответствует наибольшая доля молекул, т. е. наиболее вероятная(наивероятнейшая)скорость V нв(такая, что двигаться с этой скоростью молекула имеет наибольшую вероятность) будет
Видим, что эта скорость отличается от среднеквадратичной
Среднеквадратичная скорость несколько больше. Для анализа распределения Максвелла удобно использовать метод анализа размерностей. В распределении молекул по величине скорости V (распределение Максвелла) есть экспонента
Величина МV 2/(2 RT), очевидно, безразмерна. Независимой переменной является V — величина (модуль) скорости молекулы. Но вспомним, ведь
Это наиболее вероятная скорость (3.35), скорость, на которой приходится максимум функции распределения, та скорость, с которой движется наибольшая доля молекул. Оценим ее в воздухе вокруг нас:
Эта огромная с нашей человеческой точки зрения скорость (для человека характерна скорость 1 м/с) является естественной единицей скоростей молекул воздуха вокруг нас. Таким образом, в действительности распределение молекул по скорости зависит от безразмерной величины V / V нв, которая представляет собой скорость молекулы, измененную в естественных для данного явления (молекулярного движения) единицах. Для записи, как вероятностей, так и количества молекул, удобно ввести безразмерную (относительную) скорость и как отношение скорости V и наиболее вероятной:
Полностью доля молекул, имеющих скорости, лежащие в интервале от V до V + dV (вероятность, что молекула имеет такую скорость), записывается в виде (3.30) или
Ее нужно переписать, введя везде наиболее вероятную скорость. Затем вычисляется постоянная А. Это можно сделать, используя условие нормировки, а именно первую из формул (3.11). Имеем
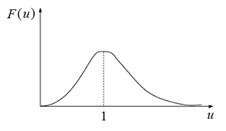
Наконец, распределение Максвелла(рис. 3.15) в наиболее естественном безразмерном виде (ведь «доля» — вероятность также безразмерна) запишется как:
Эта формула наиболее компактная и самая универсальная, т. е. в ней не проявляются несущественные для данного явления величины вроде молярной массы или температуры (хотя эти величины могут быть очень существенны для нас — пользователей этой формулы).
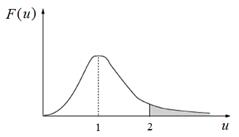
Рис. 3.15. Распределение Максвелла в безразмерной форме (в естественных единицах) Распределение Максвелла имеет множество применений. Например, для определения возможности и скорости химической реакции важно знать тепловой эффект реакции. Распределение Максвелла позволяет понять роль теплового эффекта. Действительно, в реакцию вступают лишь те молекулы, которые преодолели энергетический барьер (примерно равный глубине энергетической ямы ε в эмпирическом потенциале Леннард–Джонса (см. гл. 3)). Число молекул с такой, достаточной для вступления в реакцию энергией определяется распределением Максвелла. Молекулы с достаточной энергией составляют так называемый хвост распределения. На рис. 3.16 хвост распределения заштрихован. Заштрихованная площадь составляет долю молекул, которые могут вступить в реакцию с барьером не более чем ε ≤ M (rV нв)2/2 Дж/моль.
Рис. 3.16. Распределение молекул по относительным скоростям. Заштрихована доля молекул, скорости которых вдвое превышают наивероятнейшую скорость
|

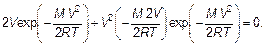 (3.33)
(3.33)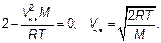 (3.34)
(3.34)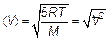 (3.35)
(3.35)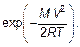 (3.36)
(3.36)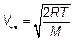 (3.37)
(3.37)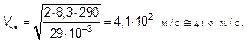 (3.38)
(3.38)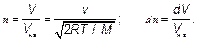 (3.39)
(3.39)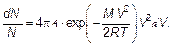 (3.40)
(3.40)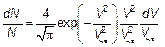 (3.41)
(3.41)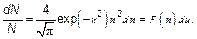 (3.42)
(3.42)