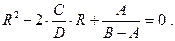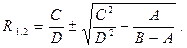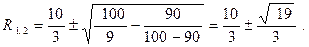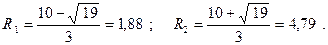Определение радиуса распространения товара
Задача 4. Фирма, занятая сбытом продукции, имеет сеть магазинов, включающую центральный магазин (главный офис) и ряд торговых точек, расположенных в радиусе 1 км вокруг этого центрального магазина. Центральный магазин реализует 90 единиц товара в месяц. В торговых точках фирма реализует 100 единиц товара. Единица товара продается по цене 10 у.д.е. При этом известно, что объем реализуемых товаров пропорционален площади территории распространения товара, а затраты на перевозку единицы товара пропорциональны расстоянию, причем коэффициент пропорциональности составляет 3 у.д.е./км · ед. Определить радиус распространения товара, при котором прибыль от продаж будет максимальной. Алгоритм решения задачи 1. Определим количество продаваемых товаров, как функцию от радиуса R их распространения: P = a + b · S, где Р – количество продаваемых товаров; S – площадь распространения товаров; a, b – коэффициенты. Коэффициент a зависит от работы центрального магазина. При R = 0 и S = 0, величина P = A, где A - количество товара, продаваемого в центральном магазине. Поэтому a = A. Коэффициент b зависит от работы остальных торговых точек. Так как в радиусе одного километра от центрального магазина в торговых точках продается B единиц товара, значение b можно определить по формуле: B = A + b · π или b = (B – A) / π. Тогда количество продаваемых товаров P = A + (B – A) · R2, так как S = π R2. Для нашей задачи Р = 90 + (100 – 90) · R2 = 90 + 10 · R2. 2. Определим прибыль от продажи товаров без учета расходов на транспортировку L: L = C · P = C · [A + (B – A) · R2], где C – цена единицы товара. Для нашей задачи L = 10 · [90 + (100 – 90) · R2] = 900 + 100 · R2. 3. Определим расходы на перевозку товаров. Для этого определим прирост товарооборота dM при предельно малом приращении радиуса – d(рис.2).
Рис.2. Прирост товарооборота при увеличении радиуса Тогда dM = [A + (B – A) · r2]dr. Интегрируя данное выражение по r в пределах от r = 0 до r = R, получим: M = A · R +1/3 · (B – A) · R3, где М – товарооборот фирмы. Для нашей задачи: M = 90 · R + 1/3 · (100 – 90) · R3 = 90 · R + 10/3 · R3. Тогда расходы на транспортировку (Т) будут равны: T = (A · R + 1/3 · (B – A) · R3) · D, где D –затраты на перевозку (коэффициент пропорциональности). Для нашей задачи Т = (90 · R + 10/3 · R3) · 3 = 270 · R + 10 · R3. 4. Определим прибыль с учетом расходов на транспортировку – П т. П т = C · [A + (B – A) · R2] – D · [A · R + 1/3 · (B – A) · R3]. Для нашей задачи: П т = 900 + 100 · R2 – 270 · R - 10 · R3 = 900 – 270 · R + 100 · R2 - 10 · R3. 5. Найдем точки экстремума функции прибыли. Для этого продифференцируем функцию прибыли и приравняем ее к нулю.
Отсюда Найдем корни уравнения:
Для нашей задачи:
Подставим значения R 1 и R 2 в формулу определения прибыли. П т (R1) = 900 – 270 · 1,88 + 100 · (1,88)2 – 10 · (1,88)3 = 679,4. П т (R2) = 900 – 270 · 4,79 + 100 · (4,79)2 – 10 · (4,79)3 = 802,1. Сравнивая значения П т, получим, что прибыль фирмы от продаж будет максимальной при радиусе распространения товара R = 4,79 км.
|

 dM = P · dr
dM = P · dr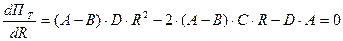 .
.