Линейной регрессии
Для уравнения зависимости потребления хлеба и хлебопродуктов от располагаемых ресурсов на человека система нормальных уравнений составит:
Решаем ее:
Рассмотрим вывод рабочих формул для расчета параметров
сократить на
Умножим уравнение (2.4) на
откуда Если в формулу (2.7) подставить
Формулы (2.5) и (2.8) удобны в том случае, если все средние уже вычислены. Рассчитаем параметры уравнения по нашим данным с помощью данных формул, имея в виду, что
Итак, отсюда, Также существует следующая формула для расчета
Итак, уравнение парной линейной регрессии, описывающее зависимость потребления хлеба и хлебопродуктов от располагаемых ресурсов на человека, рассчитанное на основе выборочного обследования домохозяйств, сгруппированных по 10 децильным группам населения, имеет вид:
Параметр В среднем по изучаемой нами совокупности (10 децильным группам населения РБ за 2008 г.) отклонение уровня располагаемых ресурсов от средней величины на 1 тыс. руб. приводило к отклонению среднего потребления хлеба и хлебопродуктов на 0,097 кг в среднем. В практическом анализе обычно говорят, что с повышением располагаемых ресурсов на 1 тыс. руб. на человека в среднем потребление хлеба и хлебопродуктов на человека увеличивается на 0,097 кг на человека в среднем. Связь прямая. Параметр По полученному уравнению определим теоретические (расчетные) значения
Рисунок 2.2 Линия регрессии зависимости потребления хлеба и хлебопродуктов на душу населения РБ от располагаемых ресурсов на человека
Показателем силы влияния фактора на результат является коэффициент эластичности: Средний коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат
Для нашего примера коэффициент эластичности составит Практически всегда фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии. Чем меньше это отличие, тем ближе будут теоретические значения подходить к эмпирическим, следовательно, тем лучше подобрано уравнение регрессии. Аппроксимация (приближение) состоит в достаточно точном воспроизведении аналитической функцией фактических данных. Чтобы оценить качество модели в целом, можно определить среднюю ошибку аппроксимации:
Модель считается подобранной достаточно хорошо, если средняя ошибка аппроксимации не превышает 8 – 10%. Для нашего примера средняя ошибка аппроксимации составит (относительные ошибки аппроксимации для каждого наблюдения рассчитаны в таблице 2.2):
Показателем тесноты прямолинейной корреляционной зависимости является коэффициент парной корреляции, показывающий, на какую часть своего среднего квадратического отклонения изменяется в среднем результативный признак при изменении факторного признака на одно среднее квадратическое отклонение. Коэффициент парной корреляции
Коэффициент корреляции может принимать значения от 0 до -1 и от 0 до +1, т.е. Для характеристики силы связи используют шкалу Чеддока.
Оценим тесноту линейной связи располагаемых ресурсов и потребления хлеба и хлебопродуктов на душу населения с помощью коэффициента корреляции:
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции – коэффициент детерминации Это означает, что 74,5% вариации потребления хлеба и хлебопродуктов обусловлены различиями в уровне располагаемых доходов населения по децильным группам, остальные 25,5% вызваны прочими факторами, которые в данном случае не рассматриваются (допустим, в нашем случае ими могут быть количество мужчин в домохозяйстве – известно, что мужчины потребляют больше хлеба, чем женщины; численность населения, принципиально не потребляющие хлеба (например, соблюдающих диету и т.д.). С помощью регрессионного анализа, когда построение функции регрессии осуществляется по данным выборки, можно получить оценки параметров зависимости. Однако они являются лишь оценками. Поэтому возникает вопрос о том, насколько они надежны, следовательно, оценки дополняются расчетом достоверности или значимости. Это объясняется возможной погрешностью, с которой определяются выборочные показатели относительно своих генеральных аналогов. Оценка значимости уравнения регрессии в целом дается с помощью F- критерия Фишера. При этом выдвигается нулевая гипотеза ( Критерий Фишера рассчитывается по следующей формуле:
Если гипотеза Фактическое значение Между критерием Фишера и коэффициентом детерминации в модели парной линейной зависимости существует связь:
В нашем примере расчет по данной формуле:
В линейной регрессии оценивается не только значимость уравнения регрессии в целом, но и значимость его отдельных параметров, а также коэффициента корреляции с помощью статистического критерия Стьюдента.. Для того чтобы осуществить такую оценку, необходимо для параметров уравнения регрессии и коэффициента корреляции рассчитать стандартные ошибки (
Чтобы оценить существенность параметров, необходимо рассчитать для них фактические значения критериев Стьюдента
Фактические значения критерия Стьюдента сравниваются с критическими (табличными) при определенном уровне значимости В нашем примере t -критерий для числа степеней свободы
В парной линейной регрессии между критерием Фишера, критериями Стьюдента коэффициентов регрессии и корреляции существует связь:
В нашем примере Имея исчисленные параметры уравнения регрессии и коэффициент парной линейной корреляции, не представляется возможным точно рассчитать уровень этих показателей в генеральной совокупности. В этом случае может идти речь с определенной вероятностью только о границах, в которых находятся параметры уравнения регрессии и коэффициент корреляции. На основе стандартных ошибок параметров и табличных значений критерия Стьюдента можно рассчитать доверительные интервалы для параметров уравнения регрессии:
Поскольку коэффициент регрессии имеет четкую экономическую интерпретацию, то доверительные границы интервала для него не должны содержать противоречивых оценок (не должны содержать положительные и отрицательные величины одновременно). В нашем примере это требование выполняется, т. е. и в генеральной совокупности (во всех домохозяйствах республики) в 2008 г. наблюдалось увеличение потребления хлеба и хлебопродуктов в зависимости от уровня располагаемых ресурсов на человека. Коэффициент корреляции в любом случае должен находиться в пределах от -1 до +1. В нашем примере это требование нарушается, поэтому принимаем, что и в генеральной совокупности связь между изучаемыми признаками была высокой. Используя уравнение регрессии, можно получить предсказываемое значение результата ( Рассчитаем точечное ожидаемое потребление хлеба и хлебопродуктов на душу населения в РБ, имея построенную модель зависимости:
Однако, точечный прогноз практически нереален на практике, поскольку эконометрика изучает экономические явления и процессы, на которые могут воздействовать огромное количество различных причин. Поэтому дополнительно необходимо осуществлять определение ошибки прогнозирования Стандартная ошибка прогнозирования рассчитывается по формуле:
Доверительный интервал прогноза:
|



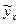
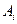
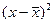
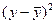
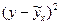
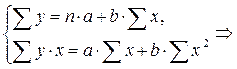
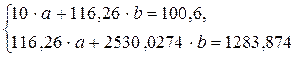 .
.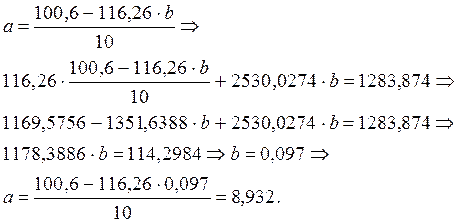
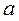 и
и  , имея в виду, что
, имея в виду, что 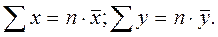 Тогда первое уравнение системы нормальных уравнений (2.3) можно записать в виде:
Тогда первое уравнение системы нормальных уравнений (2.3) можно записать в виде: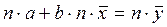 , (2.4)
, (2.4)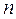 :
: 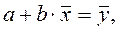 откуда получаем формулу
откуда получаем формулу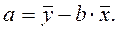 (2.5)
(2.5)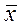 и вычтем из второго уравнения системы (2.3):
и вычтем из второго уравнения системы (2.3):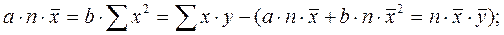 (2.6)
(2.6)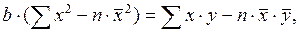
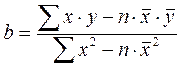 (2.7)
(2.7)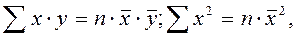 то имеем
то имеем (2.8)
(2.8)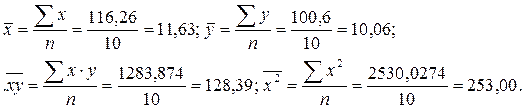
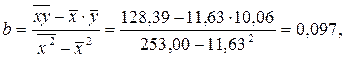
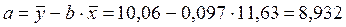 .
.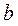 :
: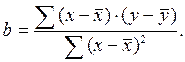 (2.9)
(2.9)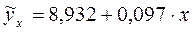 .
.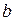 называется коэффициентом регрессии и показывает среднее изменение результата с изменением фактора на одну единицу его измерения. При
называется коэффициентом регрессии и показывает среднее изменение результата с изменением фактора на одну единицу его измерения. При 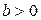 - связь прямая (при увеличении фактора результат повышается, линия регрессии является возрастающей), при
- связь прямая (при увеличении фактора результат повышается, линия регрессии является возрастающей), при 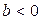 - обратная (при увеличении фактора результат уменьшается, линия регрессии имеет отрицательный наклон), при
- обратная (при увеличении фактора результат уменьшается, линия регрессии имеет отрицательный наклон), при 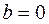 связь отсутствует. Коэффициент регрессии является именованной величиной, его значения не имеют ограничений.
связь отсутствует. Коэффициент регрессии является именованной величиной, его значения не имеют ограничений.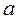 показывает значение результативного признака
показывает значение результативного признака 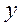 , если факторный признак
, если факторный признак 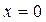 . Он именуется свободным членом, в нем определенным образом отражается среднее влияние неучтенных факторов. В том случае, если признак-фактор
. Он именуется свободным членом, в нем определенным образом отражается среднее влияние неучтенных факторов. В том случае, если признак-фактор 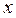 не имеет или не может иметь нулевого значения, то такая трактовка свободного члена бессмысленна. Тогда говорят, что параметр
не имеет или не может иметь нулевого значения, то такая трактовка свободного члена бессмысленна. Тогда говорят, что параметр 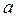 экономического смысла не имеет.
экономического смысла не имеет.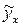 и запишем их в таблице 2.2. Правильность расчета параметров уравнения регрессии может быть проверена с помощью сравнения сумм
и запишем их в таблице 2.2. Правильность расчета параметров уравнения регрессии может быть проверена с помощью сравнения сумм 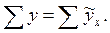 Изобразим полученное уравнение на графике – построим линию регрессии (рисунок 2.2).
Изобразим полученное уравнение на графике – построим линию регрессии (рисунок 2.2).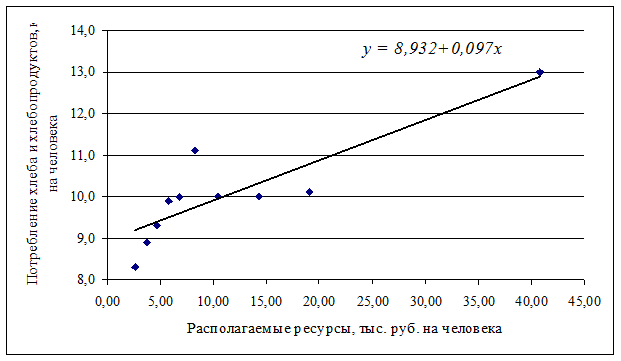
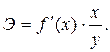
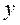 от своей средней величины при изменении фактора
от своей средней величины при изменении фактора 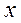 на 1% от своего среднего значения. Для прямолинейной зависимости коэффициент эластичности рассчитывается по формуле
на 1% от своего среднего значения. Для прямолинейной зависимости коэффициент эластичности рассчитывается по формуле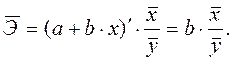 (2.10)
(2.10)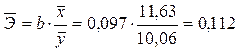 , т.е. при повышении располагаемых ресурсов на 1 человека в среднем на 1% потребление хлеба и хлебопродуктов на 1 человека увеличивается на 0,112%.
, т.е. при повышении располагаемых ресурсов на 1 человека в среднем на 1% потребление хлеба и хлебопродуктов на 1 человека увеличивается на 0,112%. (2.11)
(2.11)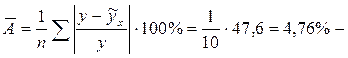 уравнение прямой линии достаточно хорошо отражает зависимость между изучаемыми явлениями.
уравнение прямой линии достаточно хорошо отражает зависимость между изучаемыми явлениями.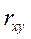 может рассчитываться по следующим тождественным формулам:
может рассчитываться по следующим тождественным формулам: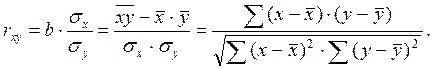 (2.12 – 2.14).
(2.12 – 2.14).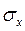 и
и 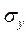 могут быть определены так:
могут быть определены так: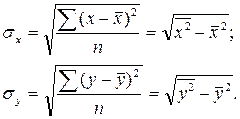 (2.15 – 2.16)
(2.15 – 2.16)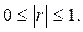 Если коэффициент корреляции
Если коэффициент корреляции 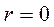 , то это означает полное отсутствие связи. Чем ближе коэффициент корреляции к 1, тем теснее связь между изучаемыми признаками. Если
, то это означает полное отсутствие связи. Чем ближе коэффициент корреляции к 1, тем теснее связь между изучаемыми признаками. Если 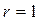 , то это максимально тесная связь, т.е. зависимость функциональная. Отрицательное значение коэффициента корреляции свидетельствует об обратной зависимости между фактором и результатом.
, то это максимально тесная связь, т.е. зависимость функциональная. Отрицательное значение коэффициента корреляции свидетельствует об обратной зависимости между фактором и результатом.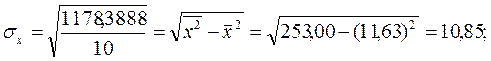
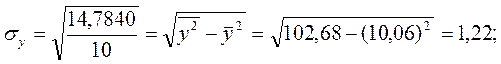
 - связь между уровнем располагаемых ресурсов и потреблением хлеба и хлебопродуктов высокая, прямая.
- связь между уровнем располагаемых ресурсов и потреблением хлеба и хлебопродуктов высокая, прямая.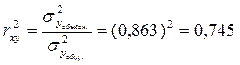 или 74,5%.
или 74,5%.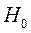 ), что коэффициент регрессии равен нулю (
), что коэффициент регрессии равен нулю (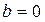 ) и, следовательно, фактор не оказывает влияния на результат, и линия регрессии параллельна оси абсцисс.
) и, следовательно, фактор не оказывает влияния на результат, и линия регрессии параллельна оси абсцисс.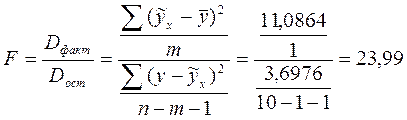 (2.17)
(2.17)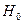 подтверждается, то уравнение регрессии незначимо. Значение критерия Фишера для конкретного случая сравнивается с критическим (табличным). Если
подтверждается, то уравнение регрессии незначимо. Значение критерия Фишера для конкретного случая сравнивается с критическим (табличным). Если 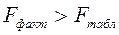 , тогда гипотеза
, тогда гипотеза 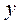 и
и 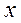 существенна и уравнение регрессии статистически значимо, т.е. фактор оказывает существенное влияние на результат. Если
существенна и уравнение регрессии статистически значимо, т.е. фактор оказывает существенное влияние на результат. Если 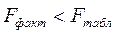 , тогда нулевая гипотеза принимается и делается вывод, что уравнение регрессии статистически незначимо, так как существует риск сделать неправильный вывод о наличии связи между
, тогда нулевая гипотеза принимается и делается вывод, что уравнение регрессии статистически незначимо, так как существует риск сделать неправильный вывод о наличии связи между 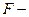 критерия Фишера, равное 23,99, больше табличного, равного 5,32, следовательно, гипотеза о случайности различий факторной и остаточной дисперсии отклоняется. Эти различия существенны, статистически значимы, уравнение надежно, значимо, показатель тесноты связи надежен и отражает устойчивую зависимость потребления хлеба и хлебопродуктов на душу населения от уровня располагаемых душевых ресурсов на человека в 10 децильных группах населения РБ в 2008 г.
критерия Фишера, равное 23,99, больше табличного, равного 5,32, следовательно, гипотеза о случайности различий факторной и остаточной дисперсии отклоняется. Эти различия существенны, статистически значимы, уравнение надежно, значимо, показатель тесноты связи надежен и отражает устойчивую зависимость потребления хлеба и хлебопродуктов на душу населения от уровня располагаемых душевых ресурсов на человека в 10 децильных группах населения РБ в 2008 г.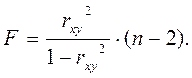 (2.18)
(2.18)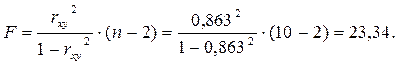
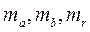 ). Эти ошибки показывают, насколько достоверно данные выборки характеризуют всю генеральную совокупность.
). Эти ошибки показывают, насколько достоверно данные выборки характеризуют всю генеральную совокупность. (2.19)
(2.19)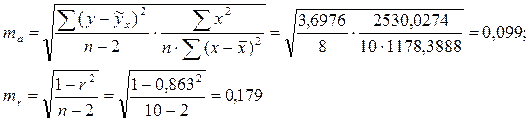 (2.20–2.21)
(2.20–2.21)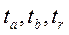 . Для параметров
. Для параметров 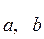 и коэффициента корреляции
и коэффициента корреляции 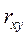 критерий Стьюдента определяет соотношение между абсолютным значением параметра и его ошибкой:
критерий Стьюдента определяет соотношение между абсолютным значением параметра и его ошибкой: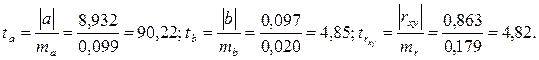 (2.22 – 2.24)
(2.22 – 2.24) и числе степеней свободы
и числе степеней свободы 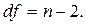 По результатам этого сравнения принимаются или отвергаются нулевые гипотезы о незначимости параметров или коэффициента корреляции. Если фактическое значение критерия Стьюдента больше табличного, тогда гипотеза о незначимости отвергается. Подтверждение значимости коэффициента регрессии равнозначно подтверждению значимости уравнения регрессии в целом.
По результатам этого сравнения принимаются или отвергаются нулевые гипотезы о незначимости параметров или коэффициента корреляции. Если фактическое значение критерия Стьюдента больше табличного, тогда гипотеза о незначимости отвергается. Подтверждение значимости коэффициента регрессии равнозначно подтверждению значимости уравнения регрессии в целом.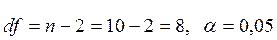 составит 2,3060.
составит 2,3060.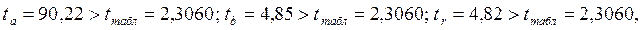 следовательно,
следовательно, 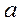 ,
, 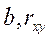 являются статистически значимыми.
являются статистически значимыми.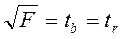 (2.25)
(2.25)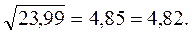
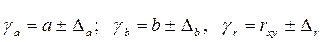 где
где 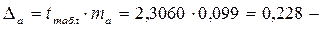 предельная ошибка параметра
предельная ошибка параметра 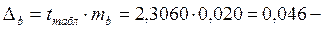 предельная ошибка коэффициента регрессии
предельная ошибка коэффициента регрессии 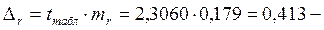 предельная ошибка коэффициента корреляции
предельная ошибка коэффициента корреляции 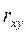 .
.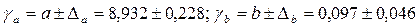 ; или
; или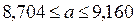 ;
; 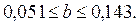
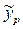 ) с помощью точечного прогноза при заданном значении фактора
) с помощью точечного прогноза при заданном значении фактора 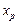 , для этого надо просто подставить в уравнение соответствующее значение
, для этого надо просто подставить в уравнение соответствующее значение 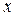 . Например, найдем потребление хлеба и хлебопродуктов в домохозяйстве, уровень располагаемых ресурсов на человека в котором на 5% больше среднего уровня по исследуемой совокупности:
. Например, найдем потребление хлеба и хлебопродуктов в домохозяйстве, уровень располагаемых ресурсов на человека в котором на 5% больше среднего уровня по исследуемой совокупности: 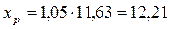 тыс. рублей на человека.
тыс. рублей на человека.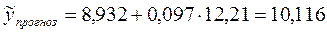 кг на душу населения.
кг на душу населения.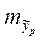 , т.е. вероятные отклонения от точечного прогноза, рассчитанного по уравнению регрессии, и интервальную оценку прогнозного значения.
, т.е. вероятные отклонения от точечного прогноза, рассчитанного по уравнению регрессии, и интервальную оценку прогнозного значения.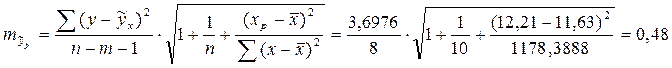 Доверительный интервал для прогнозируемого значения рассчитывается:
Доверительный интервал для прогнозируемого значения рассчитывается: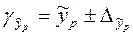 , где
, где 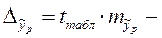 предельная ошибка прогноза, которая в 95% случаев не будет превышена.
предельная ошибка прогноза, которая в 95% случаев не будет превышена.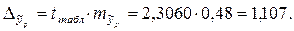
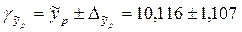 , т.е. прогнозное значение потребления хлеба и хлебопродуктов человека, располагающего 12,21 тыс. руб. ресурсов в месяц, будет находиться в интервале
, т.е. прогнозное значение потребления хлеба и хлебопродуктов человека, располагающего 12,21 тыс. руб. ресурсов в месяц, будет находиться в интервале 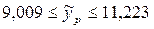 кг. Это то интервальное значение потребления хлеба и хлебопродуктов при заданном прогнозном значении уровня располагаемых душевых ресурсов, который в 95 случаях из 100 подтвердится.
кг. Это то интервальное значение потребления хлеба и хлебопродуктов при заданном прогнозном значении уровня располагаемых душевых ресурсов, который в 95 случаях из 100 подтвердится.


