В ППП Excel
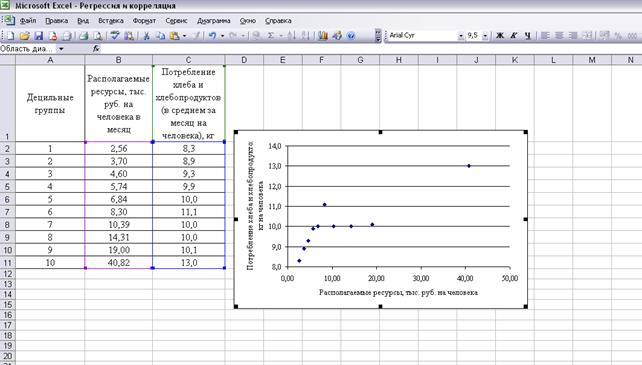
Задание 1. 1. Загрузите Excel. 2. Введите данные в таблицу. На первом листе Excel по колонкам введите значения Х и У, взятые из таблицы 2.1. Размещение таблицы показано на рисунке 1. 3. Постройте график зависимости У от Х. 1) Выделите всю таблицу с названиями колонок. Курсор мышки поставьте на ячейку А1, нажмите левую клавишу мышки и протяните курсор до ячейки В11, отпустите кнопку мыши. 2) Постройте диаграмму «Точечная». На панели инструментов щелкните пиктограмму «Добавить диаграмму», выберите на вкладке «Стандартные» тип диаграммы «Точечная». Результат действий (после небольшого оформления диаграммы) представлен на рисунке 3.1.
Рисунок 3.2 Таблица данных и график зависимости У от Х.
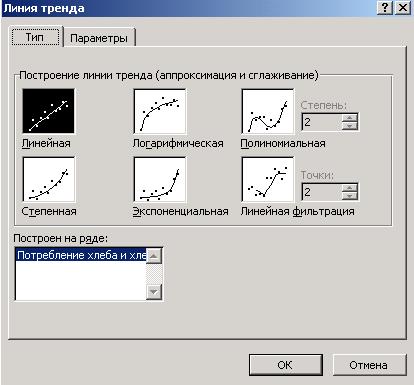
Задание 2. 1. Выделите построенный график (встаньте курсором мушки на область построенной диаграммы, щелкните левой клавишей мыши). На панели инструментов в строке главного меню вместо кнопки «Данные» появится кнопка «Диаграмма». Щелкните кнопкой «Диаграмма», выберите в ниспадающем меню пункт «Добавить линию тренда», на экране появится окно «Линия тренда», изображенное на рисунке 3.3.
Рисунок 3.3 Окно «Линия тренда» 2. Для построения графика линейной зависимости выберите тип тренда «линейная», щелкните кнопкой вкладки «Параметры», установите параметры, показанные на рисунке 3.4, нажмите кнопку «ОК».
Рисунок 3.4 Параметры «Линия тренда» На экране появится изображение, представленное на рисунке 3.5 (после небольшого элементарного оформления).
Рисунок 3.5 Результат построения парной линейной регрессии Аналогично можно построить и вывести уравнения остальных уравнений (логарифмической, полиномиальной второй степени, степенной, экспоненциальной). Получатся следующие графики (рисунок 3.6 – 3.9).
Рисунок 3.6 Уравнение логарифмической функции зависимости потребления хлеба и хлебопродуктов от уровня располагаемых ресурсов в 2008г.
Рисунок 3.7 Уравнение полиномиальной функции второй степени зависимости потребления хлеба и хлебопродуктов от уровня располагаемых ресурсов в 2008г.
Рисунок 3.8 Уравнение степенной функции зависимости потребления хлеба и хлебопродуктов от уровня располагаемых ресурсов в 2008 г.
Рисунок 3.9 Уравнение экспоненциальной функции зависимости потребления хлеба и хлебопродуктов от уровня располагаемых ресурсов в 2008 г.
Задание 3. С использованием коэффициента детерминации (согласно терминологии Excel, это коэффициент достоверности аппроксимации), определим наилучшую модель для описания зависимости результата от фактора.
Таблица 3.1 Результаты построения функций зависимости
Результаты расчетов показывают, что наибольший коэффициент детерминации имеет степенная функция (0,7554), следовательно, данная функция наиболее лучше описывает исходную зависимость.
Задание 4. Практически все эконометрические модели можно идентифицировать с помощью функции «Линейн», поэтому эту функцию следует хорошо знать. Функция «Линейн» имеет следующие достоинства: - при изменении исходных данных происходит автоматический перерасчет этой функции; - результаты расчетов содержат необходимую информацию, чтобы проверить достоверность модели и ее коэффициентов; - имеется возможность присвоить свободному коэффициенту уравнения регрессии значение, равное нулю. Функция «Линейн» имеет следующие недостатки: - процедура расчетов плохо запоминается; - не выдаются точечный и интервальный прогноз; - не выдаются доверительные интервалы уравнения регрессии; - не выдаются критические значения критериев Фишера и Стьюдента.
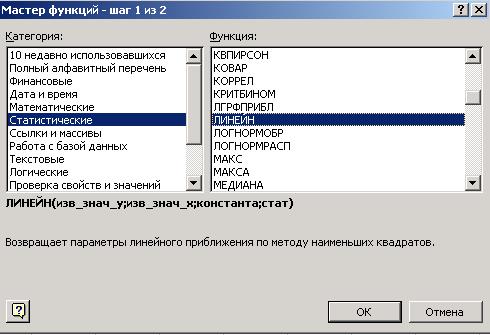
Построим уравнение парной линейной зависимости потребления хлеба и хлебопродуктов от располагаемых ресурсов в ППП Excel с помощью встроенной статистической функции «ЛИНЕЙН». Встроенная статистическая функция «ЛИНЕЙН» определяет параметры линейной регрессии 1) введите исходные данные (Таблица 2.1) или откройте существующий файл, содержащий анализируемые данные (или скопируйте данные в файле, в котором выполнялись первые два задания, на новый лист того же файла); 2) выделите область пустых ячеек 5х2 (5 строк, 2 столбца) с целью вывода результатов регрессионной статистики или область 1х2 – для получения только оценок коэффициентов регрессии; 3) активизируйте «Мастер функций» любым из способов: а) в главном меню выберите Вставка/Функция; б) на панели инструментов Стандартная щелкните по кнопке Вставка функции; 4) в окне «Категория» (Рисунок 3.10) выберите Статистические, в окне «Функция» – ЛИНЕЙН. Щелкните по кнопке OK;
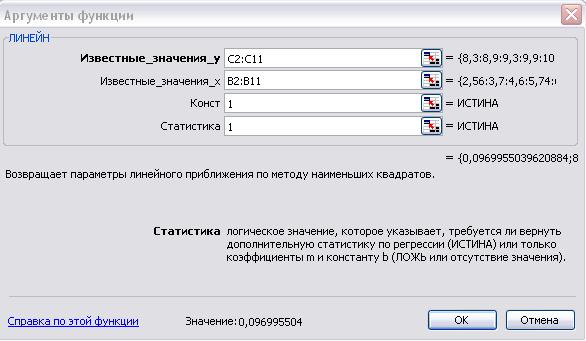
Рисунок 3.10 Диалоговое окно «Мастер функций» 5) заполните аргументы функции (рисунок 10): Известные_значения_у – диапазон, содержащий данные результативного признака; Известные_значения_х - диапазон, содержащий данные независимого признака; Константа – логическое значение, указывающее на наличие или отсутствие свободного члена в уравнении; при Константе = 1 свободный член рассчитывается обычным способом; при Константе = 0 свободный член равен 0; Статистика – логическое значение, указывающее на возможность вывода дополнительной информации по регрессионному анализу. При Статистике = 1 дополнительная информация выводится, при Статистике = 0 выводятся только оценки параметров уравнения. Щелкните по кнопке OK;
Рисунок 3.11 Диалоговое окно ввода аргументов функции ЛИНЕЙН. 6) в левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу <F2>, <CTRL> + <SHIFT> + <ENTER>. Дополнительная регрессионная статистика будет выводиться в следующем порядке:
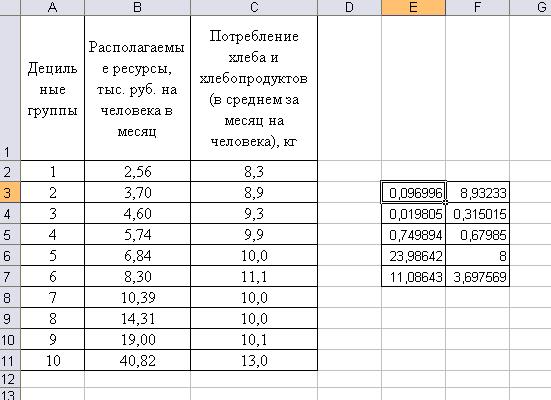
В нашем примере эти данные выглядят следующим образом (рисунок 3.12):
Рисунок 3.12 Результаты расчетов по функции «ЛИНЕЙН»
Как можно увидеть, результаты расчетов в Excel и наших расчетов вручную с применением формул, а также построения прямой на поле корреляции совпадают.
Далее построим уравнение парной линейной зависимости потребления хлеба и хлебопродуктов от располагаемых ресурсов в ППП Excel с помощью инструмента анализа данных «Регрессия». С помощью инструмента анализа данных Регрессия, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Порядок действий следующий: 1) проверьте доступ к пакету анализа. В главном меню последовательно выберите Сервис / Надстройки. Установите флажок Пакет анализа (рис. 3.13);
Рисунок 3.13 Подключение надстройки Пакет анализа
2) в главном меню выберите Сервис / Анализ данных / Регрессия. Щелкните по кнопке ОК; 3) заполните диалоговое окно ввода данных и параметров вывода (рисунок 3.14): Входной интервал Y – диапазон, содержащий данные результативного признака; Входной интервал Х – диапазон, содержащий данные независимого признака; Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет; Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении; Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона; Новый рабочий лист – можно задать произвольное имя нового листа. Чтобы получить информацию и графики остатков, установите соответствующие флажки в диалоговом окне. Щелкните по кнопке ОК.
Рисунок 3.14 Диалоговое окно ввода параметров инструмента Регрессия
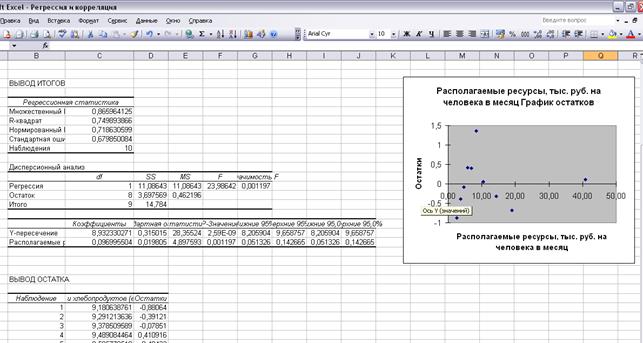
Результаты регрессионного анализа для нашего примера представлены на рисунке 3.15.
Рисунок 3.15 Результаты применения инструмента Регрессия Пояснения к рисунку 14. · Множественный R – коэффициент корреляции (множественный в случае множественной корреляции, в нашем случае это парный коэффициент корреляции между х и у). · R – квадрат – коэффициент детерминации. · Нормированный R – квадрат – коэффициент детерминации с поправкой на число степеней свободы. · Стандартная ошибка – ошибка модели. · Наблюдений – число наблюдений, по которым строится модель (в нашем случае это число групп населения). · df – число степеней свободы (строка Регрессия – для факторной (объясненной сумы квадратов отклонений), строка Остаток – для остаточной (необъясненной суммы квадратов отклонений), строка Итого – для общей суммы квадратов отклонений). · SS – значение вариации или сумма квадратов отклонений; · MS – дисперсия, деленная на соответствующее число степеней свободы. · F – критерий Фишера. · Значимость F – вероятность совершить ошибку при отклонении нулевой гипотезы: модель является незначимой. Если значимость модели проверяется на уровне значимости, равном 0,05 (как обычно мы принимаем в расчетах), то для нашего примера значимость F равна 0,001, что меньше 0,05, следовательно, модель является значимой. · «У – пересечение» – означает свободный член уравнения регрессии «а». · «Располагаемые ресурсы, тыс.руб. на человека в месяц (в общем случае пишется Переменная х» – значение коэффициента регрессии. · Стандартная ошибка – ошибка коэффициента (свободного члена или коэффициент регрессии по соответствующим строкам). · t – статистика – критерий Стьюдента для коэффициента; · «Р – значение» – уровень значимости критерия Стьюдента. · «Нижние 95%», «Верхние 95%» – нижние и верхние 95% доверительные интервалы нахождения математических ожиданий коэффициентов модели; · Предсказанное потребление хлеба и хлебопродуктов в среднем за месяц на человека (в общем случае пишется Предсказанное У) – расчетные значения У.
|







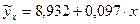
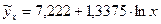


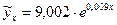
 . Порядок вычисления следующий:
. Порядок вычисления следующий: