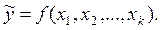Теоретическая часть. Современная наука исходит из того, что явления и процессы объективного мира органически связаны между собой
Современная наука исходит из того, что явления и процессы объективного мира органически связаны между собой, зависят друг от друга и обусловливают друг друга. Различают два типа связей между явлениями и их признаками: функциональную, или жестко детерминированную, и статистическую, или стохастически детерминированную. Если с изменением значений одной из переменных вторая изменяется строго определенным образом, т.е. значению одной переменной обязательно соответствует одно или несколько точно заданных значений другой переменной, то связь между ними является функциональной. Это полная и точная связь (например, между площадью круга и его радиусом). Стохастическая связь – это связь между случайными величинами, проявляющаяся в том, что при изменении одной из них меняется закон распределения другой, т.е. равным значениям одной переменной соответствуют разные распределения значений другой переменной. Корреляционная связь – это частный случай статистической связи, при котором разным значениям одной переменной соответствуют различные средние значения другой. Корреляционную связь можно выделить только в виде общей тенденции при массовом изучении факторов. Она является свободной, неполной и неточной связью, и может быть установлена только в среднем, при прочих равных условиях путем элиминирования влияния факторов, не являющихся предметом конкретного исследования. Функция регрессии В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии. Простая регрессия представляет собой модель, где среднее значение зависимой (объясняемой) переменной Множественная регрессия представляет собой модель, где среднее значение зависимой (объясняемой) переменной Корреляционно-регрессионный анализ занимает центральное место во всем математико-статистическом инструментарии эконометрики. Задача корреляционного анализа состоит в количественном определении тесноты связи между двумя признаками (при парной связи) и между результативным и несколькими факторными признаками при многофакторной связи и статистической оценке надежности установленной связи. Регрессионный анализ заключается в определении аналитического выражения связи (формы связи, под которой понимают тип аналитической формулы, выражающей зависимость между изучаемыми факторами (признаками). Уравнение корреляционной связи (уравнение регрессии) – это аналитическое уравнение, с помощью которого выражается зависимость между факторами.
|

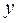 по
по 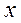 - это функция
- это функция 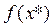 , которая описывает изменение условного среднего значения результирующей переменной
, которая описывает изменение условного среднего значения результирующей переменной 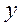 (при условии, что значения объясняющих переменных
(при условии, что значения объясняющих переменных 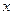 зафиксированы на уровнях
зафиксированы на уровнях 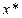 ) в зависимости от изменения значений
) в зависимости от изменения значений 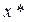 объясняющих переменных. Математически это определение может быть записано в виде
объясняющих переменных. Математически это определение может быть записано в виде 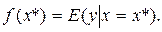
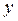 рассматривается как функция одной независимой (объясняющей) переменной
рассматривается как функция одной независимой (объясняющей) переменной 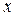 , т.е. это модель вида
, т.е. это модель вида 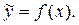
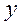 рассматривается как функция нескольких независимых (объясняющих) переменных
рассматривается как функция нескольких независимых (объясняющих) переменных 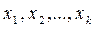 , т.е. это модель вида
, т.е. это модель вида