Построение и интерпретация модели парной линейной регрессии и корреляции
Порядок выполнения работы 1 узнать у преподавателя номер своего варианта (вид продукта) и выписать данные из таблицы А1 Приложения А 2 используя разобранный пример в качестве образца, построить модель парной линейной регрессии и корреляции, рассчитать все показатели направления и тесноты связи, оценить значимость модели в целом и ее параметров, выполнить прогноз потребления продукта при предположении, что прогнозное значение располагаемых ресурсов на 10% больше его среднего значения Содержание работы
Модели линейной регрессии, в которых переменные имеют первую степень (модели, линейные по переменным), а параметры выступают в виде коэффициентов при этих переменных (модели, линейные по параметрам), находят широкое применение в эконометрике ввиду четкой экономической интерпретации их параметров, а также потому, что многие зависимости, нелинейные на большом интервале значений факторов, близки к линейным на малом наблюдаемом интервале. В парной линейной регрессии связь между переменными определяется следующим образом:
Пусть у нас есть набор значений двух переменных Таблица 2.1 Исходные данные
Каждое из наблюдений характеризуется двумя переменными
Рисунок 2.1 Поле корреляции. Зависимость потребления хлеба и хлебопродуктов от располагаемых душевых ресурсов В этом случае наилучшей считается такая функция, график которой проходит через наибольшее количество точек или как можно ближе к ним. При оценке параметров Суть МНК заключается в том, что отыскиваются такие значения параметров уравнения: свободного члена уравнения регрессии Для того, чтобы найти минимум этой функции, надо вычислить частные производные по каждому из параметров
Решая данную систему нормальных уравнений либо методом последовательного исключения переменных, либо методом определителей, найдем искомые оценки параметров Таблица 2.2 Расчетные данные для построения модели парной
|

 (2.1), или, иначе, линейная регрессия сводится к нахождению уравнения вида
(2.1), или, иначе, линейная регрессия сводится к нахождению уравнения вида . (2.2)
. (2.2) и
и 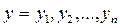 , где
, где  число наблюдений. Например, имеется информация по результатам обследования домохозяйств 10 децильных групп населения Республики Башкортостан за 2008 г. (таблица 2.1).
число наблюдений. Например, имеется информация по результатам обследования домохозяйств 10 децильных групп населения Республики Башкортостан за 2008 г. (таблица 2.1).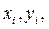 которые изобразим точками на плоскости (рисунок 2.1). Такое графическое построение называется полем корреляции.
которые изобразим точками на плоскости (рисунок 2.1). Такое графическое построение называется полем корреляции.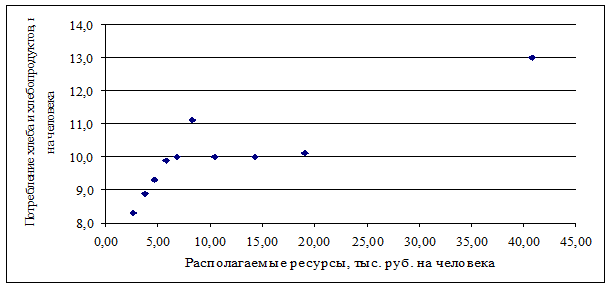
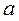 и
и  уравнения парной линейной регрессии чаще всего применяется традиционный метод наименьших квадратов (МНК). Этот метод позволяет получить оценки параметров регрессии, соответствующие определенным критериям: несмещенности (несмещенность оценки означает, что математическое ожидание остатков равно нулю), эффективности (дисперсия должна быть наименьшей), состоятельности (повышение точности оценок с увеличением объема выборки). Условия, необходимые для получения несмещенных, состоятельных и эффективных оценок, служат предпосылками МНК.
уравнения парной линейной регрессии чаще всего применяется традиционный метод наименьших квадратов (МНК). Этот метод позволяет получить оценки параметров регрессии, соответствующие определенным критериям: несмещенности (несмещенность оценки означает, что математическое ожидание остатков равно нулю), эффективности (дисперсия должна быть наименьшей), состоятельности (повышение точности оценок с увеличением объема выборки). Условия, необходимые для получения несмещенных, состоятельных и эффективных оценок, служат предпосылками МНК.
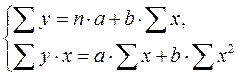 . (2.3)
. (2.3)


