Задания для самостоятельного решения. Упражнение 5.1.Найти длины сторон и координаты точек, лежащих на серединах сторон, для треугольника с вершинами:
Упражнение 5.1. Найти длины сторон и координаты точек, лежащих на серединах сторон, для треугольника с вершинами: a ) A(2;0), B(4;3), C(3;6); b ) A(2;-1), B(4;3), C(-2;1); c ) A(-2;4), B(5;-1), C(2;3). Упражнение 5.2. Найти координаты вершин и длины медиан в треугольнике, стороны которого заданы уравнениями: А),,; b),,. Упражнение 5.3. Найти координаты точки пересечения медиан в треугольнике с вершинами A(-4;2), B(2;-5), C(5;0). Упражнение 5.4. Написать уравнение прямой, проходящей через заданную точку A и образующей с положительным направлением оси OX угол 1) A(2;3), 4) A(5;-6), Упражнение 5.5. Написать уравнение прямой, проходящей через заданные точки A и B, выписать ее угловой коэффициент и координаты вектора нормали:
Упражнение 5.6. Определить угол между прямыми:
Упражнение 5.7. Найти среди прямых параллельные и перпендикулярные: 1) 2) 3) Упражнение 5.8. Написать уравнения прямых, проходящих через заданную точку параллельно и перпендикулярно заданной прямой. 1) A(2;3), 3) A(3;-6), 5) A(-2;0), Упражнение 5.9. Найти координаты вершин треугольника, образованного прямыми Упражнение 5.10. Привести общие уравнения прямых к уравнениям в отрезках, построить прямые: 1) Упражнение 5.11. В треугольнике с заданными вершинами найти уравнения сторон и высот, длины медиан и средних линий. 1) A(5;3), B(2;3), C(0;-3) 2) A(-3;7), B(7;1), C(-1;-1). Упражнение 5.12. Написать параметрическое уравнение прямой, проходящей через указанную точку параллельно заданному вектору, привести уравнение к общему виду: 1) A(2;3), Упражнение 5.13. Решить графически систему линейных неравенств:
Упражнение 5.14. Записать канонические и параметрические уравнения прямой, проходящей через заданную точкупараллельно заданному вектору; привести к общему виду: a) A(4;3;2), Упражнение 5.15. Записать канонические и параметрические уравнения прямой, проходящей через заданные точки, привести к общему виду: 1) A(-1;2;3), B(2;6;-1); 2) A(3;-1;4), B(1;3;2). Упражнение 5.16. Составить уравнение плоскости, проходящей через три заданных точки: 1) A(-1;2;3), B(2;6;-1), C(1;3;0); 2) A(3;-1;4), B(3;3;2), C(3;2;-1). СОДЕРЖАНИЕ ВВЕДЕНИЕ 3 § 1. ПРЕОБРАЗОВАНИЯ МАТРИЦ 4 1.1. Предварительные сведения. 4 1.2. Арифметические действия с матрицами. 5 1.3. Элементарные преобразования матриц. 7 1.4. Задания для самостоятельного решения. 9 § 2. ОПРЕДЕЛИТЕЛИ КВАДРАТНЫХ МАТРИЦ. ТЕОРЕМА КРАМЕРА 12 2.1. Вычисление определителей. 12 2.2. Приложения определителей к решению систем линейных уравнений. 16 2.3. Задания для самостоятельного решения. 17 § 3. ОБРАТНЫЕ МАТРИЦЫ 19 3.1. Определения и примеры. 19 3.2. Поиск обратной матрицы с помощью метода Гаусса 19 3.3. Поиск обратной матрицы с помощью алгебраических дополнений к элементам исходной матрицы. 20 3.4. Задания для самостоятельного решения. 22 § 4. ОБЩАЯ ТЕОРИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ........................................................................................ 24 4.1. Основные обозначения. 24 4.2. Классификация систем линейных алгебраических уравнений. 25 4.3. Алгоритм метода Гаусса. 26 4.4. Метод обратной матрицы. 29 4.5. Задания для самостоятельного решения. 30 § 5. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ 32 5.1. Предварительные сведения. 32 5.2. Прямая на плоскости. 32 5.3. Угол между прямыми. 35 5.4. Составление уравнений прямых. 36 5.5. Полуплоскости и системы линейных неравенств. 39 5.6. Прямая и плоскость в пространстве. 41 5.7. Задания для самостоятельного решения. 43
|

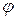 .
.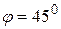 ; 2) A(-4;5),
; 2) A(-4;5), 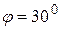 ; 3) A(-1;-3),
; 3) A(-1;-3),  ;
;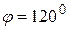 ; 5) A(0;0),
; 5) A(0;0), 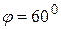 ; 6) A(-1;0),
; 6) A(-1;0), 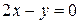 ,
, 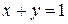
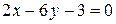 ,
, 
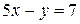 ,
, 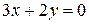
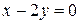 ,
, 
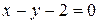
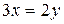 ,
, 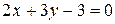
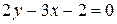 ,
,  ,
, 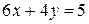 ,
, 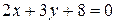
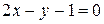 ,
, 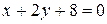 ,
, 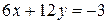 ,
, 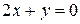
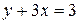 ,
, 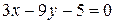 ,
,  ,
, 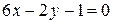
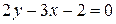 ; 2) A(-1;5),
; 2) A(-1;5), 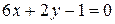 ; 6) A(0;3),
; 6) A(0;3), 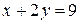 ,
,  ,
, 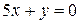 . Построить треугольник, найти тангенсы его углов и координаты точки пересечения высот.
. Построить треугольник, найти тангенсы его углов и координаты точки пересечения высот.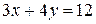 ; 2)
; 2) 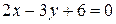 ; 3)
; 3) 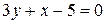 .
.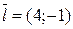 ; 2) A(-1;5),
; 2) A(-1;5), 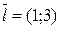 ; 3) A(-2;3),
; 3) A(-2;3), 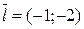 .
.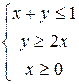
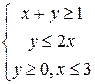
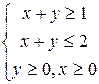
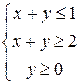
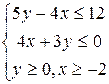
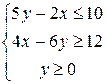
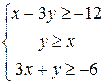
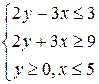
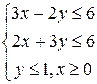
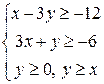
 ; b) A(-2;-3;1),
; b) A(-2;-3;1), 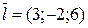 .
.


